13. Soluzioni del 4 ottobre 2021 – Elezioni, voti disgiunti e duelli a tre

Le soluzioni del 4 ottobre 2021 a cura di Fabio Ciuffoli 

Ieri mattina abbiamo proposto due problema sulle sfide elettorali e oggi presentiamo le soluzioni. 

Elezioni, voti disgiunti e duelli a tre – soluzioni 

1. Voti disgiunti. In un Comune con 100.000 elettori, 60.000 hanno votato la lista liberale, mentre gli altri hanno votato la lista democratica. Inoltre, poiché è possibile il voto disgiunto, tra voto alla lista e voto al candidato sindaco, 6.000 elettori liberali hanno dato la loro preferenza al candidato sindaco democratico e 5.000 elettori democratici hanno votato il candidato sindaco liberale. Se scegliamo a caso un elettore che ha votato il candidato sindaco liberale, qual è la probabilità che si tratti di un democratico?

1. SOLUZIONE. La probabilità è del 8,5%. Per la dimostrazione utilizziamo uno schema.

• Voti lista liberale: 60.000
• Voti lista democratica:  40.00.
• Voti sindaco liberale: 59.000; 
• Voti sindaco democratico: 41.000; 

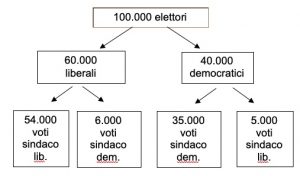
I voti per il sindaco liberali sono in totale 59.000 di cui 54.000 espressi dai liberali e 5.000 dai democratici. Il rapporto 5.000/59.000 = 0,085 quindi 8,5% è la percentuale di democratici che ha votato per il sindaco liberale sul totale dei voti per il sindaco liberale.

2. Duello a tre. Tre avversari: Ascani, Brunetti e Colli, sono impegnati in un duello a tre. Ogni avversario ha un colpo a disposizione: prima Ascani, poi Brunetti ed infine Colli. Terminato il primo turno, i sopravvissuti hanno diritto ad ulteriori colpi nella stessa sequenza. Per ogni sfidante il miglior risultato è essere l’unico sopravvissuto. Il secondo miglior risultato è di essere uno dei due sopravvissuti. Il terzo risultato è rappresentato dalla possibilità che nessuno muoia. Il peggiore è sicuramente quello di venire uccisi.

Si sa che: Ascani non è un buon tiratore e ha soltanto il 30% di possibilità di colpire la persona a cui mira; Brunetti tira molto meglio raggiungendo una precisione dell’80%; Colli è un tiratore nato non sbaglia mai un colpo.

• Qual è la miglior strategia di Ascani al primo turno?
• Chi ha la maggior possibilità di sopravvivenza e quali sono le probabilità di ciascuno di sopravvivere?

2. SOLUZIONE. La miglior strategia di Ascani al primo turno è sparare in alto. Le probabilità di sopravvivere sono:  Ascani = 34%;  Brunetti = 52%;  Colli = 14%.

Se Ascani sparasse a Brunetti e lo colpisse, firmerebbe la sua condanna a morte, poiché Colli non sbaglia mai un colpo. Se Ascani sparasse a Colli e lo colpisse, allora Brunetti sparerà ad Ascani con una probabilità di sopravvivenza di Ascani inferiore al 20%. Per queste ragioni la strategia migliore per Ascani è quella di sparare in aria. Di seguito Brunetti sparerà a Colli e se lo manca, Colli ucciderà Brunetti. Al secondo turno Ascani potrà sparare nuovamente e visto che rimane soltanto un’altra persona egli avrà almeno il 30% di probabilità di sopravvivere. In particolare Colli, pur essendo il più preciso, ha le minori probabilità di sopravvivenza cioè 20 – (20 * 30/100) = 14%; Brunetti avrà il 52% circa, mentre Ascani, che parte svantaggiato sulla carta, avrà il 34% circa. Il procedimento di calcolo può essere illustrato con lo schema seguente, nel quale calcoliamo la probabilità di morire di ciascun partecipante e poi il suo complemento, che equivale alla probabilità di sopravvivere. Indichiamo con A, B e C rispettivamente Ascani, Brunetti e Colli.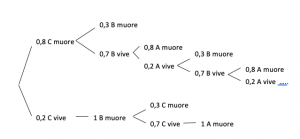 

La probabilità di Ascani di morire equivale a (0,2 * 0,7) + (0,8 * 0,7 * 0,8) + (0,8 * 0,7 * 0,2 * 0,7 * 0,8) + (…) ≈ 0,66
quindi probabilità di sopravvivere 1 – 0,66 ≈ 0,34.

La probabilità di Brunetti di morire equivale a 0,2 + (0,8 * 0,3) + (0,8 * 0,7 * 0,2 * 0,3) + (…) ≈ 0,48
quindi probabilità di sopravvivere 1 – 0,47 ≈ 0,52.

La probabilità di Colli di morire equivale a 0,8 + (0,2 * 0,3) = 0,86
quindi probabilità di sopravvivere 1 – 0,86 = 0,14.

La morale del problema è che per i pesci piccoli è meglio passare il primo turno per diventare dei campioni. Lo si vede spesso in politica. Ad esempio, durante le competizioni elettorali, può essere vantaggioso attendere e salire alla ribalta soltanto quando gli altri si sono fatti fuori a vicenda, eliminandosi dalla gara.

A lunedì prossimo