Menu
Le soluzioni del 12 luglio 2021 a cura di Fabio Ciuffoli
Cognac, wasan e triangoli
Le soluzioni dei giochi pubblicati ieri.
1. LA BOTTIGLIA DI COGNAC. La bottiglia di cognac ha un’altezza di 27 cm, un diametro di 7 cm e capacità massima di 750 centimetri cubi. Come molte bottiglie ha una rientranza nella parte inferiore, mentre è perfettamente simmetrica rispetto all’asse verticale.
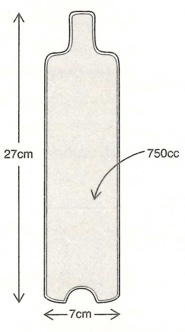
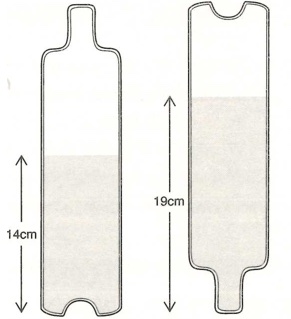
La bottiglia contiene cognac fino ad un’altezza di 14 cm e quando viene capovolta, l’altezza del cognac è di 19 cm. Quanto cognac c’è nella bottiglia, in centimetri cubi?
Ricordiamo che il volume di un cilindro si ottiene con la formula (π r2 h) dove r è il raggio e h è l’altezza.1. SOLUZIONE LA BOTTIGLIA DI COGNAC. E’ un gioco interessante perché si può risolvere con il semplice insight: pensare alla parte vuota come se fosse piena. Quando la bottiglia contiene cognac all’altezza di 14 cm, significa che ci sono 13 cm vuoti. Se, capovolgendo la bottiglia, l’altezza fosse esattamente 13 cm, allora la bottiglia sarebbe piena per metà. Nel nostro caso, l’altezza nella bottiglia capovolta è 19 cm quindi è superiore alla metà. Ora ipotizziamo di togliere un centimetro di altezza di cognac: nell’immagine a sinistra, il livello scenderebbe a 13 cm e la parte vuota diventerebbe 14 cm mentre, nell’immagine a destra, l’altezza diventerebbe 18 cm. Procediamo togliendo gradualmente 1 cm di livello di cognac, fino a quando l’altezza della parte vuota a sinistra diventerà uguale all’altezza del cognac a destra. A quel punto la bottiglia sarà piena per metà e ciò accade quando togliamo 3 cm di cognac. Infatti se riducessimo a 11 cm il livello di cognac, ci sarebbero 16 cm sopra senza cognac e la bottiglia capovolta conterrebbe ora 19 – 3 = 16 cm di cognac. La parte vuota e quella piena sarebbero uguali, quindi la bottiglia sarebbe piena per metà!* In sintesi, il cognac nella bottiglia è uguale a metà del volume più 3 cm di altezza. La bottiglia ha una capacità di 750 cc, quindi la metà è 375 cc. Il volume di 3 cm di cognac è 3,14 *3,52 *3 = 115 cc circa. Infine, sommando, il cognac in bottiglia è 375 + 115 = 490 cc circa.
*[La quantità da togliere si calcola (19 – 13)/2 = 3 cm. Ovviamente se il livello del cognac fosse inferiore alla metà, i calcoli sarebbe gli stessi ma con segno negativo]
2. WASAN Matematica giapponese divertente e partecipativa. E’ autunno e nel giardino cadono le foglie. Al mattino del primo ottobre sono cadute 10 foglie, che vengono raccolte; al mattino seguente sono cadute altre 40 foglie, che vengono a loro volta raccolte; al mattino del terzo giorno sono cadute altre 90 foglie che, vengono raccolte; al mattino del 4 ottobre ci sono 160 altre foglie e via di seguito. Con il passare dei giorni, sempre più foglie si staccano dall’albero. Qual è il numero di foglie cadute fino al mattino del 15 ottobre?
2. SOLUZIONE WASAN matematica giapponese divertente e partecipativa. Organizziamo le informazioni e cerchiamo uno schema ricorrente.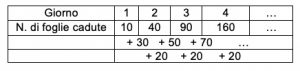
Ogni giorno le foglie cadute aumentano di 30, 50, 70 e via di seguito, mostrando un incremento regolare di 20 foglie per ciascun giorno. Ora con l’ampliamento dello schema fino al 15 ottobre si arriva al calcolo delle foglie totali, sommando il numero di foglie cadute al giorno dal 1° al 15 ottobre
10 + 40 + 90 + 160 + 250 + … + … = 12.400.
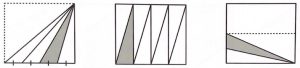
3. OTTO TRIANGOLI. Su due lati di un quadrato sono stati individuati punti equidistanti in modo da formare otto triangoli con un vertice condiviso. Quale frazione del quadrato è ombreggiata in rosso?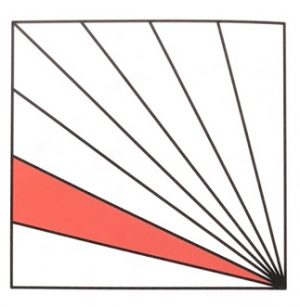
3. SOLUZIONE OTTO TRIANGOLI. Gli otto triangoli hanno la stessa base (un quarto di lato) e la stessa altezza (lato del quadrato) quindi hanno tutti la stessa area. L’area ombreggiata rappresenta perciò un ottavo del quadrato.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
8 risposte
Io per il quesito 2 ho ragionato così. Ho indicato con x la quantità di cognac
Ho immaginato di ruotare di 180 gradi la bottiglia di destra e di sovrapporla a quella di sinistra.
Ho quindi usato una sorta di formula di Graasmann, dicendo che 2x, meno una colonnina di 6 cm di cognac, dà la capacità totale della bottiglia.
In questo caso l’incognita è il volume di cognac nella bottiglia…. Lo stesso problema a volte chiede di calcolare la capacità della bottiglia a partire dai dati dei due livelli di cognac, per i quali basterebbe un righello. Ad esempio nel libro Gli enigmi di Mosca di B Kordemsky il problema n 193 è di questo tipo.
Soluzione algebrica al problema 2. Si tratta della somma dei quadrati dei numeri naturali da 1 a 15 moltiplicando per 10 il risultato finale. Indicando con n i giorni, le foglie cadute fino a quel giorno sono [n*(n+1)*(2n+1) /6 ] * 10. Con n = 15 il risultato è 12.400.
Per il primo quesito, se chiamiamo x il volume della parte vuota della bottiglia, sappiamo che occupa un’altezza di 13 cm nella bottiglia rovesciata. Quindi il volume totale della bottiglia sarà uguale a 2x + un cilindro di altezza 6 cm. Svolgendo i calcoli: 2x = 750 – ( 3,5^2 * π * 6 ) = 519,09 con x = 259,54. Il volume del cognac sarà quindi 750 – 259,54 = 490,45
Per il secondo quesito per ogni giorno i il numero di foglie cadute è maggiore di i^2 * 10 rispetto al giorno precedente.
Nel mio caso sono giunto alla soluzione del quesito 1 con un ragionamento diverso.
Ho calcolato il volume di un cilindro con diametro 7 e altezza 27 ed ho calcolato il volume delle parti vuote (attorno al collo e nel fondo della bottiglia) 1039,08 – 750 = 289,08. A questo punto la differenza di altezza (5cm) a bottiglia capovolta corrisponde alla differenza di volume vuoto del collo bottiglia rispetto al fondo: 5 * 3,5^2 * π =192,42. Pertanto il volume sottratto alla bottiglia dall’incavo del fondo è dato da: (289,08 – 192,42)/2 = 48,33 e quello sottratto dalla cima della bottiglia 192,42 + 48,33 = 240,75.
A questo punto il volume cercato a botiglia dritta è dato da: 14 * 3,5^2 * π – 48,33 = 490,45353.
Anche a bottiglia capovolta si ha: 19 * 3,5^2 * π – 240,75 = 490,45353
Quesito “cognac”: risolto con un sistema di 1° grado di due equazioni (indipendenti) in 2 incognite.
Quesito “foglie”: è una serie di ragione x(i)= 2*x(i-1)-x(i-2)+20 (provare usando il foglio elettronico)
Quesito “triangolo rosso”: tutti gli 8 triangoli hanno pari base (1/8 del lato) e Pari altezza (il lato), hanno tutti pari area, perciò l’area del triangolo rosso è 1/8 dell’area del quadrato.
Ciao Fabio, continua così!
Nello, prezioso collaboratore, anche a distanza. Attendiamo proposte, ciao.
A mio avviso la serie indicata è valida solo per i che va da 2 a n e non tiene conto del valore di partenza del giorno 1 in quanto restituisce sempre 20.
La serie corretta è:
x(i) = x(1) + x(i-1) + k * (i – 1)
dove x(1) è il valore iniziale di foglie al giorno 1, k è la costante di incremento (valore della derivata seconda della serie). Nel caso del quesito in esame si ha x(1) = 10 e k = 20 e la soluzione è data dalla sommatoria di x(i) con i che va da 1 a 15.