
I Giochi del Lunedì di Prisma dell’11 agosto 2025 a cura di Fabio Ciuffoli
Oggi proponiamo due problemi con riquadri e i numeri contenuti al loro interno. Un gioco di caselle e di combinazioni possibili e un piacevole intrattenimento in questo clima di mezzo agosto. Invitiamo i lettori inviarci osservazioni e proposte di soluzione utilizzando lo spazio dei commenti. Domani alle ora 17.00 pubblicheremo le soluzioni.
Numeri e riquadri
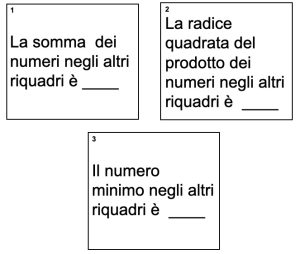
2. I quattro quadrati in figura formano un diagramma di Venn con dieci regioni etichettate da A a J. Le lettere da A a J rappresentano ciascuna un numero compreso tra 1 e 10, in modo tale che non esistano due regioni con lo stesso numero e vengano utilizzati tutti i numeri da 1 a 10. La somma delle regioni in ciascun quadrato dà lo stesso numero. Che valore ha D, che è l’intersezione di tutti e quattro i quadrati?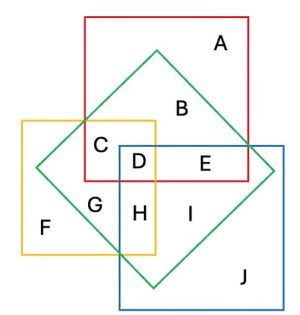
Aggiornamento per le soluzioni click qui.
I problemi sono tratti da The Mathematical Playground: People and Problems from 31 Years of Math Horizons, 2024. Math Horizons è la rivista universitaria della Mathematical Association of America e il libro è una raccolta dei suoi migliori enigmi con ottimo materiale per studenti e docenti.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
13 risposte
La soluzione A = 8, B = 2, C = 5, D = 7, E = 6, F = 9, G = 3, H = 4, I = 1, J = 10 sembra soddisfare tutte le condizioni con S=28 se non sbaglio ancora:
Quadrato Rosso (A+B+C+D+E): 8+2+5+7+6=28 ✅
Quadrato Giallo (C+D+F+G+H): 5+7+9+3+4=28 ✅
Quadrato Verde (B+C+D+E+G+H+I): 2+5+7+6+3+4+1=28 ✅
Quadrato Blu (D+E+H+I+J): 7+6+4+1+10=28 ✅
Trovata considerando la somma dei numeri che non si trovano in un determinato quadrato (cioè la somma totale, 55, meno la somma di quel quadrato, S) deve essere uguale alla somma dei numeri che si trovano solo in quel quadrato e le condizioni imposte sui quattro quadrati.
Ottimo è il metodo che ho usato anche io e prevede più di una combinazione possibile ma D è sempre 7. Sono uscite le soluzioni al link sopra.
Solo per riempire un vuoto ma senza grossi meriti: nel problema 2, D = 7 (brute force). 😉
Be’ il merito c’è tutto, rischiare di restare irrisolto. Grz
* rischiava
Al problema 1, Se si considerano le etichette: (5,0,0) e (12,6,1)
N. 1. Siano x,y,z i numeri scritti nei riquadri 1,2,3.
y+z=x
√xz=y.
z=min{x,y}
Se min{x,y}=x => z=x => y=0 => √x²=0
Se min{x,y}=y =>. z=y.=> x=2y => √(2y²)=y
In entrambi i casi (x,y,z)=(0,0,0)
Problema 2. L’unico valore di D che permette di far combaciare tutte le somme e rispettare la condizione che ogni lettera sia un numero diverso da 1 a 10 è D=5.
Buongiorno Sergio, ho visto la tua soluzione e c’è qualcosa che non va. Nella tua proposta , la somma dei valori nei quattro quadrati dà quattro risultati diversi: 22, 25, 39 e 40. Mentre il testo dice “La somma delle regioni in ciascun quadrato dà lo stesso numero”. Forse possono esserci altre interpretazioni?
Hai ragione, devo aver sbagliato qualcosa, adesso ricontrollo i calcoli con la mente un po’ più fresca di ieri notte!
Problema 1. A prima vista sembrerebbe che esiste un solo modo possibile per cui tutte e tre le frasi siano verificate, ed è quando i numeri in tutte e tre le frasi sono uguali a 0. Ma forse è meglio approfondire!?
Considerando i numeri presenti nei riquadri trovo una soluzione che è 12,6,1
e un’altra simil banale 5,0,0 da trascurare se i numeri devono essere tutti diversi.
Ottime considerazioni e soluzioni, mi sono permesso un piccolo scherzo di ferragosto non rigorosamente matematico 😉. A domani per tt le soluzioni