154. Giochi del 28 luglio 2025 – Bandiere e matematica

I Giochi del Lunedì di Prisma del 28 luglio 2025  a cura di Fabio Ciuffoli

In questi giorni, esattamente il 1° agosto, si celebra la festa della bandiera svizzera che ricorda la fondazione della Confederazione Elvetica del 1291. Prendiamo spunto da questa festa per proporre due problemi geometrici sulle originali bandiere nazionali della Svizzera e anche del Nepal. La storia delle bandiere è molto interessante e rivela diversi aspetti: storici, politici, sociali, simbolici e anche matematici. Ad esempio il tricolore italiano, comparso per la prima volta nel 1797 nella Repubblica Cispadana, è un rettangolo di proporzioni base/altezza 3:2 composto da tre fasce verticali di uguale area nei colori verde, bianco e rosso, come definito dall’articolo 12 della Costituzione del 1947 e viene festeggiato il 7 gennaio. In genere tutte le bandiere hanno forma rettangolare, seppure di varie proporzioni, tranne quelle di Svizzera e Città del Vaticano, che hanno forme quadrate, e quella del Nepal che ha la forma di due triangoli sovrapposti. Le dimensioni, le forme e i colori sono definiti per legge da ogni Stato e in alcuni casi rivelano un preciso utilizzo delle geometria. Speriamo di aver stimolato qualche curiosità o riflessione tra nostri lettori, che Invitiamo comunque a inviarci osservazioni, proposte simili e soluzioni utilizzando lo spazio dei commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.  

Bandiere e matematica

1. Secondo la Risoluzione Federale del 12 dicembre 1989 la bandiera svizzera mostra una croce greca bianca i cui bracci, eguali fra di loro sono di un sesto più lunghi che larghi, su uno sfondo quadrato rosso. Il margine tra un braccio e il lato della bandiera deve essere della stessa larghezza del braccio, in modo che l’altezza totale della croce sia 20:32 dell’altezza del lato della bandiera. In altri termini la misura del margine è 6:32 del lato della bandiera.

Qual è il rapporto dell’area bianca della croce sul totale dell’area della bandiera?

Una spinta: per visualizzare la bandiera con le proporzioni in 32esimi click qui.

2. La descrizione per la costruzione della bandiera nepalese, con dovizia di dettagli geometrici, è riportata nell’articolo 8 della Costituzione del 2015.

Riportiamo di seguito una sintesi delle norme corredate dal relativo disegno.

1. Sulla parte inferiore di un panno cremisi tracciare un segmento AB
2. Tracciare dal punto A un segmento AC perpendicolare ad AB, in maniera che AC sia uguale ad AB, più un terzo di AB. Su AC individuare il punto D in maniera che il segmento AD sia uguale al segmento AB. Unire B a D.
3. Sul segmento BD individuare il punto E in modo che BE sia uguale ad AB.
4. Tracciare il segmento FG parallelo e della stessa lunghezza di AB e passante per E.
5. Unire C a G.

Sapendo che il segmento AB misura 1 metro, calcolare il perimetro della bandiera, definito dai segmenti che congiungono C, G, E, B, A, C. [Non si considera il bordo blu]

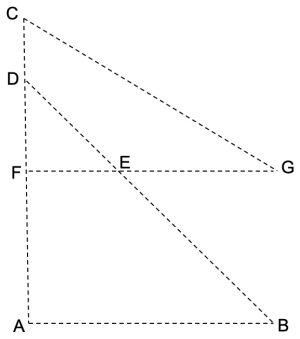Ci sembra un bell’esercizio matematico per i piccoli cittadini nepalesi, che immaginiamo sui banchi delle scuole primarie, impegnati a sviluppare calcoli e disegni. 

Alcune particolarità. La bandiera del Nepal, adottata nel 1962 dal nuovo governo costituzionale, ha la forma di un doppio triangolo rettangolo che raffigura l’unione di due bandierine triangolari rappresentanti i rami di una dinastia che governava dal XIX secolo. Il colore di fondo è cremisi come il rododendro, il fiore nazionale, simbolo della vittoria che contrasta con il  bordo è blu, simbolo della pace. Infine, a simboleggiare la permanenza in cielo, su entrambi i rettangoli compaiono le immagini stilizzate della mezzaluna e del sole. L’aspetto più incredibile di questa bandiera è che le due ipotenuse dei triangoli rettangoli non sono parallele.

Una spinta: per visualizzare la descrizione completa per la costruzione della bandiera nepalese, suddivisa in ventiquattro stadi click qui. 

Aggiornamento per le soluzioni click qui.

I Giochi del Lunedì di Prisma tornano tra due settimane.