153. Soluzioni del 14 luglio 2025 – Il ritorno di Cheryl

Le soluzioni del 14 luglio 2025 a cura di Fabio Ciuffoli

Ieri abbiamo presentato un recente problema dal titolo ”Il numero civico di Cheryl” proposto da Joseph Yeo, docente presso il National Institute of Education di Singapore, già autore 10 anni fa del famoso “Problema del compleanno di Cheryl”. Abbiamo proposto anche altri due problemi che nel 2015 suscitarono un notevole confronto on line. Di seguito pubblichiamo le soluzioni.

Il ritorno di Cheryl – soluzioni 

1. Il numero civico di Cheryl. Cheryl dice ai suoi due amici Albert e Bernard: “Ho pensato a due numeri diversi di una cifra ciascuno compresi tra 0 e 9. L’ultima cifra del prodotto dei due numeri è la stessa dell’ultima cifra del numero civico di Bernard. Qual è la somma di questi due numeri?”

• Albert: “Non so qual è il numero civico di Bernard.”
• Bernard: “Ovviamente, conosco il numero civico della mia casa e so con certezza qual è la somma dei due numeri.”
• Albert: “All’inizio non sapevo qual era la somma dei due numeri, ma ora lo so.”

Qual è la somma dei due numeri?

1. SOLUZIONE. Siano a e b i due numeri pensati da Cheryl. Riportiamo in tabella: nella prima colonna i possibili valori per la cifra finale di (a • b); nella seconda colonna le possibili coppie il cui prodotto ha quella cifra finale e nella terza colonna possibili somme (a + b).

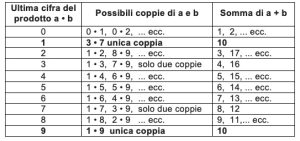
Supponiamo, come nell’esempio proposto, che il numero civico di Bernard finisca con 4. Cheryl potrebbe aver pensato 1 e 4 (1 • 4 = 4), oppure 3 e 8 oppure (3 • 8 = 24) o ancora 6 e 9 (6 • 9 = 54). La somma a + b potrebbe essere 5 o 11 o 15, ecc. per cui Bernard non potrebbe conoscere con certezza la somma (a + b).L’unica ipotesi in cui Bernard può dichiarare di conoscere la somma dei due numeri, come egli dichiara, è quando c’è una sola possibilità (a + b). Osservando la tabella, si deduce che ciò si verifica quando l’ultima cifra è 1 o 9. In entrambi i casi, la somma è 10. A questo punto anche Albert può dichiarare di conoscere la somma dei due numeri.

2. Un gioco da ragazzi. Inserire le cifre da 1 a 9 nelle nove caselle vuote dello schema “a forma di serpente” in figura, senza mai ripetere la stessa cifra e rispettando l’ordine delle operazioni: moltiplicazione, divisione, addizione e sottrazione.

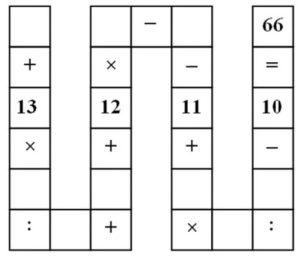
2. SOLUZIONE. Si tratta di un problema a prove e errori, con più soluzioni possibili, un lavoro empirico piuttosto meccanico e noioso ma, con un po’ di algebra, è possibile snellire lo svolgimento. Riscriviamo il “serpentone” mediante un’equazione indicando con le lettere (a, b, c, d, …. i) le nove cifre da inserire nelle caselle vuote. Iniziamo dall’alto a sinistra e avremo:

a + (13b/c) + d + 12e – f – 11 + (gh/i) – 10 = 66

con alcuni passaggi

a + (13b/c) + d + 12e – f +(gh/i) = 66 + 11 + 10 = 87

ancora

a + d – f + (13b/c) + 12e +(gh/i) = 87

Ora possiamo supporre che (b/c) e (gh/i) siano numeri interi e che (13b/c) non sia troppo grande. A questo punto iniziamo a inserire i numeri empiricamente. C’è più di una soluzione, quindi ci sono diverse ipotesi che porteranno alla disposizione corretta.  [Si potrebbe scrivere un programma per calcolare il numero possibile di soluzioni corrette che sono più di 100].

Per mantenere il termine (13b/c) il più piccolo possibile, abbiamo posto

b = 2 e c = 1 perciò

a + d – f + 26 + 12e +(gh/i) = 87

svolgendo

a + d – f + 12e +(gh/i) = 61

I numeri rimanenti sono le cifre da 3 a 9. Includono i numeri primi 3, 5 e 7 che, per non complicare gli altri termini, li poniamo: a = 3, d = 5 e f = 7.

A questo punto avremo:  3 + 5 – 7 + 12e +(gh/i) = 61

svolgendo

12e +(gh/i) = 60

I numeri rimanenti sono 4, 6, 8, 9.

Procediamo per tentativi e avremo: e = 4; g = 9; h = 8; i = 6  quindi

48 + (72/6) = 48 +12 = 60

Ci sono alcuni enigmi che si risolvono con un lampo di intuizione, e altri, come questo, in cui non c’è alternativa se non il metodo per tentativi ed errori.

Infine due brevi note: 1. Il problema non è semplice, in particolare per ragazzi di otto anni, basti pensare che le possibili combinazioni delle 9 cifre, ossia il numero delle permutazioni semplici senza ripetizione, sono 362.880  [P_n = n!]. 2. Il Vietnam ottiene ottimi risultati nelle classifiche internazionali PISA che confrontano i risultati dei quindicenni in matematica, scienze e lettura. Il Vietnam si classifica al 17° posto in matematica e all’8° in scienze, superando molti paesi occidentali come il Regno Unito (26° e 20° posto) e gli Stati Uniti (36° e 28° posto).

3. I dolci di Hannah. Hannah ha uno zaino che contiene n caramelle, sei delle quali sono arancioni e il resto (n – 6) sono gialle. La ragazza estrae due caramelle e le mangia. La probabilità che abbia mangiato due caramelle arancioni è pari a 1/3. Sulla base di ciò, mostrare che n² – n – 90 = 0.

3. SOLUZIONE. La probabilità di pescare una caramella arancione da uno zaino che contiene n caramelle, di cui 6 sono arancioni, è 6/n. Al secondo tentativo, ci saranno n – 1 caramelle e 6 – 1 = 5 caramelle arancioni, perciò la probabilità di pescare una caramella arancione è 5 / (n – 1). La probabilità totale di pescare una caramella arancione la prima volta e un’altra caramella arancione la seconda volta è pari al prodotto delle probabilità singole (è un po’ come calcolare la probabilità che si ottenga due volte testa lanciando due volte consecutivamente una moneta), ovvero:

(6/n) • (5 / (n-1) = 30 / (n² –n)

Sappiamo che tale probabilità è uguale a 1/3, dunque abbiamo la seguente equazione:

30 / (n² – n) = 1/3

A questo punto, supponendo n diverso da 0 e n diverso da 1, altrimenti il denominatore si annullerebbe – ipotesi supportata dal fatto che sappiamo esserci più di una caramella nello zaino – moltiplichiamo entrambi i membri dell’equazione per (n² – n). In questo modo otteniamo:

30 = (n² – n) / 3

ora moltiplicando entrambi i membri per 3:

90 = n² – n

da cui n²  – n – 90  = 0

[L’equazione di secondo grado ha due soluzioni (10; -9) lo zaino contiene 10 caramelle].

I Giochi del Lunedì tornano tra due settimane.