
I Giochi del Lunedì di Prisma del 14 luglio 2025 a cura di Fabio Ciuffoli
Dieci anni fa è stato pubblicato il famoso “Problema del compleanno di Cheryl” che ha fatto parte delle Olimpiadi di Matematica di Singapore per ragazzi di 14 anni. Il problema originale prevedeva che Cheryl facesse una dichiarazione e che Albert e Bernard parlassero di seguito. Se volete rinfrescarvi la memoria, in fondo alla pagina trovate il relativo link.
Recentemente il suo autore, Joseph Yeo docente presso il National Institute of Education di Singapore, ha pubblicato un problema simile ”Il numero civico di Cheryl” che proponiamo di seguito.
Completiamo questa puntata riproponendo altri due problemi che nel 2015 suscitarono un acceso dibattito on line: “Un Gioco da Ragazzi” proposto da un insegnante vietnamita ai suoi allievi di otto anni e “I Dolci di Hannah” proposto da uno studente britannico.
Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio dei commenti. Domani alle ore 17.00 pubblicheremo la soluzione.
Il ritorno di Cheryl
1. Il numero civico di Cheryl. Cheryl dice ai suoi due amici Albert e Bernard: “Ho pensato a due numeri diversi di una cifra ciascuno compresi tra 0 e 9. L’ultima cifra del prodotto dei due numeri è la stessa dell’ultima cifra del numero civico di Bernard. Qual è la somma di questi due numeri?”
Qual è la somma dei due numeri?
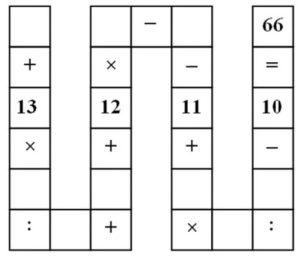
2. Un gioco da ragazzi. Inserire le cifre da 1 a 9 nelle nove caselle vuote dello schema “a forma di serpente” in figura, senza mai ripetere la stessa cifra e rispettando l’ordine delle operazioni: moltiplicazione, divisione, addizione e sottrazione.
3. I dolci di Hannah. Hannah ha uno zaino che contiene n caramelle, sei delle quali sono arancioni e il resto (n – 6) sono gialle. La ragazza estrae due caramelle e le mangia. La probabilità che abbia mangiato due caramelle arancioni è pari a 1/3. Sulla base di ciò, mostrare che n2 – n – 90 = 0.
Il compleanno di Cheryl (2015)
Il problema 1 è stato proposto da Joseph Yeo docente presso il National Institute of Education di Singapore.
Nell’immagine in evidenza il National Institute of Education di Singapore.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
4 risposte
1. I numeri sono o 1 e 9 oppure 3 e 7. La somma è comunque 10.
2. Di soluzioni ce ne sono parecchie. Cercandole via software se ne trovano 128. Questa è una:
1 + 13 x 2 : 6 + 4 + 12 x 7 – 8 – 11 + 3 x 5 : 9 – 10 = 6.
3. 6/n * 5/(n-1) = 1/3 -> n = 10.
Ottimo Giorgio. Il problema 2 ha diverse soluzioni ed è complesso, in particolare per raggazzi di otto anni, ma molto interessante ai fini didattici e del ragionamento per prove e errori. A domani per tt le soluzioni commentate.
Problema 1.
Ci provo.
Tra i prodotti delle coppie di numeri compresi tra 0 e 9, risulta solo un numero di due cifre tale che l’ultima sua cifra sia diversa da tutti gli altri prodotti: il 21, cioè 3*7
Detto in altri termini: 3 e 7 è l’unica coppia il cui prodotto è individuabile dall’ultima cifra; tra le altre coppie ce ne sono più di due che condividono l’ultima cifra del loro prodotto.
La risposta al quesito è allora: 10
NB: a rigore, ci sarebbe anche la coppia 1 e 9 che presenta l’unico prodotto terminante per la cifra 9.
Ma anche la somma 1+9 dà 10, che è comunque la risposta al quesito di Cheryl.
Ottimo Vic, a domani per le soluzioni commentate.