152. Soluzioni del 30 giugno 2025 – I mietitori di Tolstoj

Soluzioni del  30 giugno 2025 a cura di Fabio Ciuffoli

Ieri abbiamo proposto due problemi matematici attribuiti al grande scrittore e filosofo russo Lev Tolstoj più altri due problemi assegnati nelle prove di matematica per studenti dei nostri giorni. E di seguito pubblichiamo le soluzioni.

I mietitori di Tolstoj – soluzioni 

1. Il cappello. Uno sconosciuto entra in un negozio e compra un cappello dal prezzo di € 10 pagando con una banconota da € 50. Il venditore non ha il resto e perciò va al negozio di fiori accanto a cambiare la banconota. La fioraia cambia la banconota con due banconote da € 20 e una da € 10. Il venditore torna al suo negozio e consegna al suo cliente il cappello e € 40 di resto. Un’ora dopo la fioraia entra e dice che la banconota da  € 50 è falsa, quindi il venditore di cappelli le dà €  50 dal suo registratore di cassa. Quanto ha perso il proprietario del negozio di cappelli?

1. SOLUZIONE. Il venditore di cappelli ha dato al cliente € 40 e un cappello,  mentre il cliente non ha dato al venditore alcun valore. Il venditore e la fioraia sono pari: si sono scambiati € 50. Infine il proprietario del negozio ha perso € 40 e un  cappello.

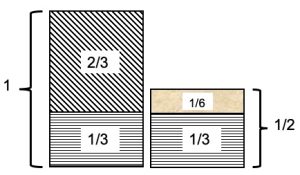
2. I mietitori. Questo problema era uno dei preferiti da Lev Tolstoj che lo illustrava con il seguente disegno. Ad una squadra di mietitori viene assegnato l’incarico di mietere due campi di grano, uno dei quali aveva superficie doppia dell’altro. La squadra si dedicò al campo più grande per mezza giornata poi si divisero a metà e nell’altra mezza giornata le due sotto-squadre lavorarono su entrambi i campi. A fine giornata il campo grande era stato mietuto completamente, mentre del campo più piccolo rimaneva ancora un pezzetto, che un mietitore terminò lavorando da solo per tutto il giorno successivo. Supponendo che i mietitori lavorassero alla stessa velocità, sapreste determinare da quanti mietitori era composta la squadra?

2. SOLUZIONE. La soluzione può essere trovata in modo algebrico o più immediatamente in modo grafico. Seguiamo questa seconda via e proponiamo il disegno in figura, quello che utilizzava Tolstoj, ponendo il campo grande pari ad 1 unità e quello piccolo a ½ unità. Se il campo grande è stato completato lavorando per mezza giornata con la squadra intera e per l’altra mezza giornata con metà squadra, significa che a metà giornata avevano completato 2/3 e nell’altra metà giornata il restante 1/3, così come l’altra squadra sul campo più piccolo vedi superficie a righe orizzontali in figura. A questo punto rimaneva 1/6 di unità che veniva completata da un mietitore in un giorno. Durante il primo giorno sono stati mietuti 4/3 di unità, che equivale ad 8/6 di unità su un totale 9/6. Per cui la squadra era composta da 8 mietitori.

3. Due aiule. Il signor Bianchi ha un campo dove coltiva pomodori e fragole in due aiuole rettangolari accostate come illustrato in figura. Quest’anno ha allungato di 3 metri uno dei lati dell’aiuola dei pomodori in modo che l’aiuola diventasse quadrata. In questo modo l’aiuola delle fragole è diminuita di 15 m². Prima di questa variazione, quanti metri quadrati misurava l’area dell’aiuola dei pomodori?

3. SOLUZIONE. Se un lato dell’area dei pomodori è stato allungato di 3 metri con un aumento di superficie di 15 m², significa che l’altro lato è di 5 m come illustrato in figura. Il quadrato dei pomodori ora sarà 5 • 5 = 25 m² quindi è stato aumentato di 15m² perciò prima della variazione era 25 – 15 = 10 m². L’aiuola dei pomodori misurava 10 m².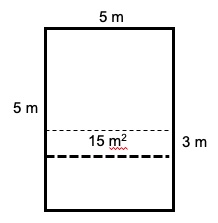

4. Mele verdi e rosse. Un melo dà solo mele verdi e un altro melo dà solo mele rosse. I contadini colsero tutti i i frutti di entrambi gli alberi e si accorsero che c’erano 5 mele rosse ogni 4 mele verdi. Ne mangiarono in totale 16 rosse e 16 verdi. Quando contarono le mele rimaste videro che ce n’erano 3 rosse ogni 2 verdi. Quante mele di ciascun colore c’erano all’inizio?

4. SOLUZIONE. Indicando con R il numero iniziale di mele rosse e con V il numero iniziale di mele verdi, avremo:

(1) R/V = 5/4 da cui R = (5/4) V

Vengono mangiate 16 Verdi e 16 Rosse, perciò le mele rimaste sono:

(R – 16 e (V – 16)

Dopo averle mangiate il rapporto è 3 rosse e 2 verdi, quindi

(2) (R – 16) / (V – 16) = 3/2

Sostituiamo R nella seconda equazione  (5/4)V – 16 / V – 16 = 3/2

Moltiplichiamo entrambi i membri per 2(V – 16)

2[(5/4)V – 16] = 3(V – 16)

svolgiamo

(10/4)V – 32 = 3V – 48

 – 32 + 48 = 3V – (10/4)V

 16 =  (12V – 10V)/4

16 = (½)V infine V = 32. 

Mele Rosse = (5/4) 32 = 40.

I Giochi del Lunedì di Prisma tornano tra due settimane.