1. La sfida dei biscotti. Alberto e Beatrice hanno di fronte due contenitori con biscotti. In un contenitore ci sono 8 biscotti al cioccolato e nell’altro 4 biscotti al limone. Ogni giocatore può prendere i biscotti in due modi:
Il giocatore che prende l’ultimo biscotto vince la partita e può tenere tutti i biscotti. Alberto inizia per primo. Quanti e quale tipo di biscotti deve prendere per vincere?
2. Pancake a colazione. Due amici sono a colazione di fronte a due pile di pancake di altezza m e n. Decidono di mangiare, a turno, dalla pila più grande un numero di pancake multiplo dei pancake nella pila più piccola. Il pancake inferiore di ogni pila è avariato e quindi chi finisce una pila è perdente. Per quali coppie m,n c’è una strategia vincente per chi inizia il gioco?
Ad esempio se le pile sono composte da 9 e da 5 pancake, il primo giocatore prende 5 pancake dalla prima pila lasciando 4 e 5, il secondo giocatore prende 4 pancake dalla seconda pila lasciando 4 e 1. A questo punto il primo giocatore prende 3 pancake dalla prima pila lasciando 1 e 1 così il secondo giocatore è costretto a prendere l’ultimo pancake di una pila è sarà perdente.
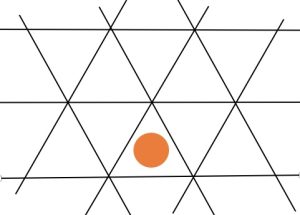
3. Tovaglia con triangoli. Due amici fanno colazione su una tovaglia disegnata con triangoli equilateri. Uno chiede all’altro quante sono le probabilità che lanciando un biscotto circolare di raggio 2 cm, si fermi all’interno del triangolo di lato 12 cm, senza toccare i lati?
La sfida dei biscotti è trattata nel libro “Head Scratcher – The puzzle book”, R. Eastaway – B. Hobbs.
Pile di pancake è una rielaborazione dal libro “Mathematical Puzzle” di P. Winkler.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
7 risposte
Per il problema 3:
l’approccio dovrebbe essere secondo me di calcolare la probabilità che il punto corrispondente al centro del biscotto ricada in un’area triangolare di lato 12-2*SQRT(3), cioè circa 5,07cm, rappresentata dal triangolo equilatero rosso in figura
Ottimo Vic, è questo il metodo da utilizzare. A domani per tt le soluzioni.
Ciao Fabio. Ti ringrazio.
Innanzitutto comunque correggo il mio errore di digitazione nella formula precedente:
il lato è 12-4*SQRT(3); il valore era però giusto: 5.07cm
Nel frattempo ho potuto fare anche i calcoli per risolvere il problema, e mi risulta che la probabilità è pari al rapporto delle aree dei due triangoli.
In ultima analisi è uguale al rapporto dei quadrati dei rispettivi lati, quindi:
P = (5,07^2) / (12^2) = 17,86%
1. Alberto prende 4 biscotti dal contenitore con quelli al cioccolato come prima mossa. Così poi qualsiasi numero di biscotti Beatrice prenda, lui può pareggiare.
Alberto deve prendere 5 biscotti al cioccolato.
No, perché resterebbero 4 e 4. A quel punto Beatrice potrebbe prenderli tutti e così vincerebbe.
la mia risposta è per Pamy Pa.