Soluzioni del 5 maggio 2025 a cura di Fabio Ciuffoli
Ieri abbiamo presentato quattro problemi con coccinelle immaginarie, che si rincorrono a partire dai vertici di figure geometriche regolari. Un modo per ragionare sui metodi di soluzione di problemi geometrici più o meno complessi. Pubblichiamo di seguito le notre proposte di soluzione.
Coccinelle e poligoni regolari – soluzioni
Iniziamo con un esempio molto semplice. Se due coccinelle, collocate agli estremi di un segmento AB di lunghezza 1, partono nello stesso istante e si muovono l’una verso l’altra alla stessa velocità costante, si incontreranno a metà segmento e ciascuna avrà percorso ½ del segmento AB come schematizzato in figura. [In questo tipo di problemi le dimensioni della coccinella sono ininfluente]
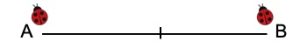
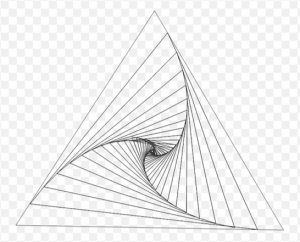
1. Immaginiamo tre coccinelle collocate ai rispettivi vertici di un triangolo equilatero di lato 1. Ogni coccinella inizia a muoversi verso la coccinella immediatamente vicina in senso orario. (Non importa se vanno in senso orario o antiorario). Le coccinelle partono nello stesso istante, corrono tutti alla stessa velocità costante e in ogni momento ogni coccinella corre direttamente verso la coccinella vicina. Durante l’inseguimento, le coccinelle corrono a spirale prima di incontrarsi tutte al centro, come schematizzato in figura. Quanto percorre ogni coccinella prima di incontrarsi con le altre?
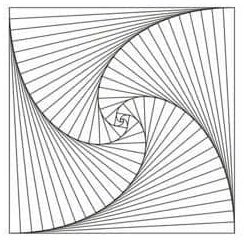
2. Quattro coccinelle sono ai quattro vertici di un quadrato di lato 1. Ogni coccinella inizia a correre verso la coccinella immediatamente vicina in senso antiorario. (Non importa se vanno in senso orario o antiorario). Le coccinelle partono alla stessa ora, corrono tutti alla stessa velocità e in ogni momento ogni coccinella corre direttamente verso la coccinella vicina. Durante l’inseguimento, le coccinelle corrono a spirale prima di incontrarsi tutte al centro, come schematizzato in figura. Quanto percorre ogni coccinella prima di incontrarsi con le altre?
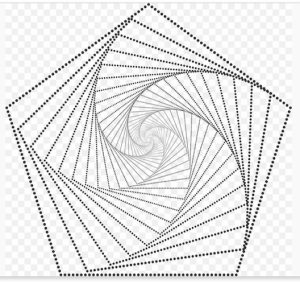
3. Cinque coccinelle sono ai cinque vertici di un pentagono regolare di lato 1. Ogni coccinella inizia a correre verso la coccinella immediatamente vicina in senso antiorario. (Non importa se vanno in senso orario o antiorario). Le coccinelle partono alla stessa ora, corrono tutti alla stessa velocità e in ogni momento ogni coccinella corre direttamente verso la coccinella vicina. Durante l’inseguimento, le coccinelle corrono a spirale prima di incontrarsi tutte al centro, come schematizzato in figura. Quanto percorre ogni coccinella prima di incontrarsi con le altre?
4. Sei coccinelle sono ai sei vertici di un esagono regolare di lato 1. Ogni coccinella inizia a correre verso la coccinella immediatamente vicina in senso antiorario. (Non importa se vanno in senso orario o antiorario). Le coccinelle partono alla stessa ora, corrono tutti alla stessa velocità e in ogni momento ogni coccinella corre direttamente verso la coccinella vicina. Durante l’inseguimento, le coccinelle corrono a spirale prima di incontrarsi tutte al centro, come schematizzato in figura. Quanto percorre ogni coccinella prima di incontrarsi con le altre?
SOLUZIONI. Sebbene il problema possa essere posto con qualsiasi poligono regolare, di solito è basato su un quadrato. In questo caso le quattro coccinelle si troveranno simultaneamente agli angoli di un quadrato che ruota costantemente, con dimensioni che diminuiscono gradualmente, finché gli insetti non si incontreranno al centro. I loro percorsi sono spirali logaritmiche. La lunghezza di ciascun percorso può essere determinata mediante calcolo infinitesimale, ma il problema può essere risolto anche in modo geometrico: in ogni momento il percorso di ciascun insetto è perpendicolare all’insetto che sta inseguendo e il quadrato immaginario va lentamente rimpicciolendosi, quindi non esiste alcuna componente del movimento di un insetto inseguito che lo porti ad avvicinarsi più che allontanarsi dal suo inseguitore. L’inseguitore raggiungerà l’inseguito nello stesso tempo che occorrerebbe se l’inseguito rimanesse stazionario e il suo inseguitore si muovesse direttamente verso di esso. Ogni percorso a spirale avrà quindi la stessa lunghezza del lato del quadrato unitario. Immaginiamo con molta fantasia che una coccinella abbia una GoPro in testa. Il filmato dell’inseguimento della coccinella vicina, lungo il percorso a spirale, sarebbe esattamente lo stesso e richiederebbe lo stesso tempo del filmato della coccinella che si muovesse direttamente lungo il lato del quadrato verso la coccinella ferma.
Un modo geometrico per misurare la distanza percorsa da ciascun insetto, questa volta applicato a un esagono regolare ma valido in generale, viene illustrato nella figura seguente.
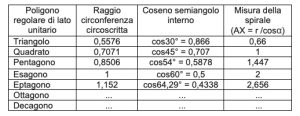
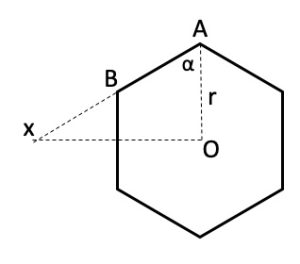A partire dall’angolo di un poligono regolare, si traccia il raggio AO fino al centro del poligono, quindi si estende OX perpendicolare rispetto ad AO finché non incontra uno dei lati o la sua estensione. Ora AX, che è r volte la secante dell’angolo α, è la misura della lunghezza percorsa da ciascun insetto. Dal triangolo rettangolo AXO, conoscendo la misura r e l’ampiezza dell’angolo α, possiamo determinare l’ipotenusa AX. Infatti AX = r/cosα = 1/0,5 = 2.
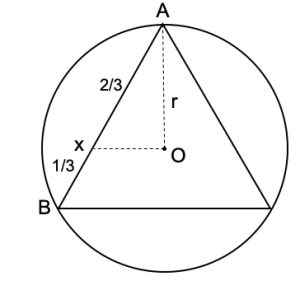
1. SOLUZIONE. Nel caso del triangolo, OX incontra AB a 2/3 da A, quindi l’insetto percorre 2/3 due della lunghezza del lato del triangolo, come illustarto in figura.
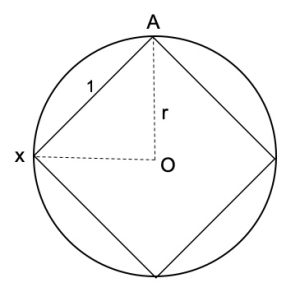
2. SOLUZIONE. Nel caso del quadrato, OX incontra il lato del quadrato esattamente nel suo vertice X, quindi l’insetto percorre esattamente un lato del quadrato, come disegnato in figura.
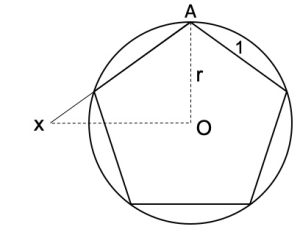
3. SOLUZIONE. Nel caso del pentagono, OX incontra il prolungamento di AB quando AX misura 1,4471 indicando che la spirale percorsa dalle coccinelle è circa un lato e mezzo del pentagono, come illustrato in figura. Infatti a partire dal lato uguale a 1, determinato il raggio r che è 0,8506. Sappiamo che il semiangolo interno in A è 54°, possiamo determinare AX = r/cos54 = 0,8506/0,5878 = 1,4471.
4. SOLUZIONE. Nel caso dell’esagono, già visto sopra, l’angolo α è 60° e AX misura 2 indicando che l’insetto percorre il doppio della misura del lato.
SOLUZIONI
Formule
Raggio della circonferenza circoscritta al poligono di lato unitario:
Angolo interno al vertice di un poligono di n lati = [(n – 2)•180°]/n
Coseno del semiangolo interno
Misura della spirale o del segmento AX = r/cosα)
Tabella riassuntiva
I Giochi del Lunedì di Prisma tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
