155. Soluzioni dell’11 agosto 2025 – Numeri e riquadri

Soluzioni dell’11 agosto 2025 a cura di Fabio Ciuffoli

Ieri abbiamo presentato due problemi con riquadri e numeri contenuti al loro interno: un gioco di caselle e di combinazioni possibili. Di seguito pubblichiamo le nostre proposte di soluzione. 

Numeri e riquadri – soluzioni 

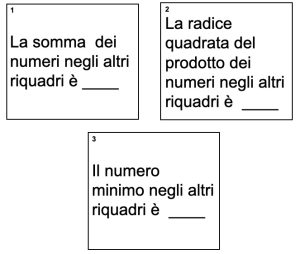
1. SOLUZIONE. Presentiamo tre soluzioni. Indichiamo con x, y e z i tre numeri. Ora se consideriamo solo i numeri negli spazi vuoti, c’è una sola possibile soluzione: x = y = z = 0.  Tuttavia, interpretando in modo creativo il testo, si può pensare a una soluzione di fantasia che include anche i numeri dei riquadri (1; 2; 3). In questo caso, ci sono due soluzioni possibili. I riquadri diventano tre equazioni: x = 5 + y + z; y = √3xz; z = min (x, y, 1).

• Supponiamo che min (x, y, 1) = y. Perciò z = y. Quindi x = 5 + 2y. E y = √3xy. Sappiamo che y è maggiore o uguale a 0, poiché è il valore di una radice quadrata, quindi y = 0. per cui la soluzione: x = 5, y = z = 0.
• Ora supponiamo che min (x, y, 1) = x. Quindi z = x e y = – 5, che è una contraddizione poiché y è maggiore o uguale a 0.
• Infine, supponiamo che min (x, y, 1) = 1, otteniamo la seconda soluzione: x = 12, y = 6, z = 1. 

2. I quattro quadrati in figura formano un diagramma di Venn con dieci regioni etichettate da A a J. Le lettere da A a J rappresentano ciascuna un numero compreso tra 1 e 10, in modo tale che non esistano due regioni con lo stesso numero e vengano utilizzati tutti i numeri da 1 a 10. La somma delle regioni in ciascun quadrato dà lo stesso numero. Che valore ha D, che è l’intersezione di tutti e quattro i quadrati?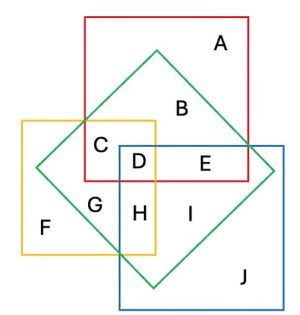

Le somme delle regioni in ciascun quadrato dà lo stesso numero, quindi A + B + C + D + E (quadrato rosso) = C + D + F + G + H (quadrato giallo) = B + C + D + E + G + H + I (quadrato verde) = D + E + H + I + J (quadrato blu).

2. SOLUZIONE. La somma delle regioni è la stessa per ogni quadrato perciò, quando due quadrati si intersecano, le regioni che non si intersecano devono essere uguali. Quindi, per i quadrati rosso e verde, che hanno in comune B, C, D, E avremo A = G + H + I. In altri termini, le due regioni ombreggiate in figura hanno lo stesso valore. Allo stesso modo, F = B + E + I. E anche J = B + C + G.

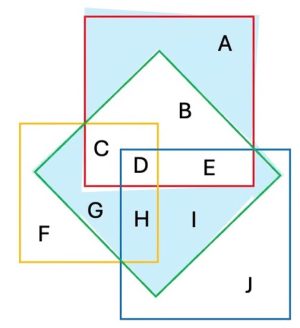
Riassumendo F + A + J = B + E + I + G + H + I + B + C + G = 2(G + I + B) + E + H + C. 

Il valore massimo di F + A + J è 10 + 9 + 8 = 27.

Il valore minimo di 2(G + I + B) + E + H + C  è 2(1 + 2 + 3) + 4 + 5 + 6 che è 27.

Entrambi questi valori sono 27. L’unico numero mancante è 7 e l’unica regione mancante è D, quindi D = 7.

I Giochi del Lunedì di Prisma tornano tra due settimane.