150. Soluzioni del 2 giugno 2025 – Geometria dall’Australia

Soluzioni del 2 giugno 2025 a cura di Fabio Ciuffoli

Ieri abbiamo presentato tre problemi di geometria tratti dalla rivista australiana “Parabola” dell’Università di Sidney che hanno stimolato interessanti e originali commenti da parte dei nostri lettori verso i quali siamo riconoscenti. Di seguito pubblichiamo le nostre proposte di soluzione. 

Geometria dell’Australia – soluzioni 

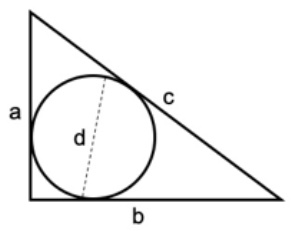
1. In figura è disegnato un cerchio di diametro d inscritto in un triangolo rettangolo di cateti a, b e di ipotenusa c. Dimostrare che d = a + b – c.

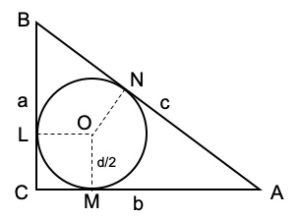
1. SOLUZIONE. Indichiamo con O il centro del cerchio e con L, M e N i punti di tangenza tra cerchio e lati del triangolo, come mostrato in figura seguente. Gli angoli in L, M e N sono rettangoli e OL = OM. Ora BL = a – (d/2) e AM = b – (d/2). I triangoli rettangoli AOM e OAN hanno l’ipotenusa in comune, cateti uguali e sono quindi congruenti perciò AN = AM = b – (d/2). Allo stesso modo BN = BL = a – (d/2). Ne segue che c = AB = AN + BN = b – (d/2) + a – (d/2) = a + b – d.

2. Sui lati esterni di un rettangolo vengono disegnati quattro triangoli equilateri come in figura. Dimostrare che la somma delle aree dei quattro triangoli bianchi è uguale all’area del rettangolo.

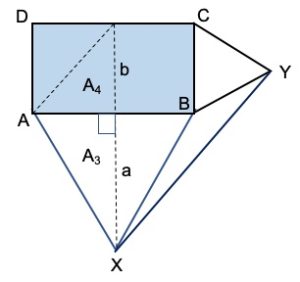
2. SOLUZIONE. Per la soluzione di questo problema, i lettori hanno proposto diversi metodi particolarmente eleganti, chiari e sintetici. Segnaliamo i commenti di Masahiro Matsuno, Massimo Molinelli, Raffaela Scognamiglio, Marco Rinetti e quello originale di Sergio Casiraghi. Di seguito illustriamo la nostra proposta di soluzione. Consideriamo la parte bassa sulla destra del disegno, che abbiamo ingrandito nelle due figure seguenti. Sappiamo che due triangoli con la stessa altezza, hanno aree proporzionali alle rispettive basi. Ora ABX è un triangolo equilatero e tutte le sue altezze a sono uguali. Il rapporto tra le aree A₁/A₂ = b/a. Allo stesso modo avremo A₃ /A₄ = a/b. Essendo A₂ = A₃ avremo Area XBY = A₁ = A₄ che è un quarto dell’area del rettangolo. Lo stesso ragionamento vale per gli altri tre quarti del disegno, quindi possiamo dedurre che la somma delle aree dei quattro triangoli bianchi è uguale all’area del rettangolo.

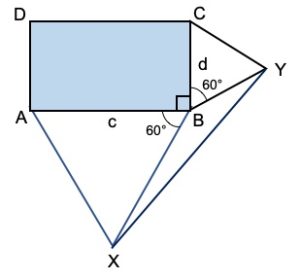
Un altro metodo per la soluzione, utilizzando la trigonometria. Sappiamo che l’area di un triangolo è data dal semiprodotto di due lati per il seno dell’angolo compreso. Ora, utilizzando i simboli in figura seguente, avremo: Area del triangolo YBX = (cd/2) sen∠ YBX.

L’angolo YBX misura (360°- 60° – 60° – 90°) = 150°. Infine, l’area del triangolo YBX = (cd/4) che è quello che volevamo dimostrare.

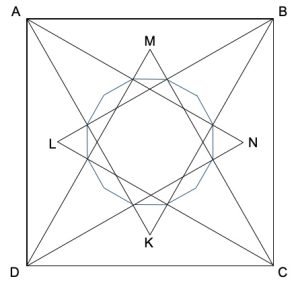
3. Quattro triangoli equilateri, ABK, BCL, CDM e DNA sono disegnati all’interno di un quadrato. Dimostrare che i quattro punti medi dei segmenti KL, LM, MN, NK e i punti medi degli otto segmenti AK, BK, BL, CL, CM, DM, DN, AN sono i dodici vertici di un dodecagono regolare.

3. SOLUZIONE. Indichiamo con O il centro del quadrato e con P e Q gli ipotetici punti medi rispettivamente dei segmenti CM e KN come in figura seguente. Dimostreremo che OP = OQ e che l’angolo POQ è di 30° quindi per simmetria, si potrà dedurre che i dodici punti sono alla stessa distanza da O, per cui il dodecagono è regolare.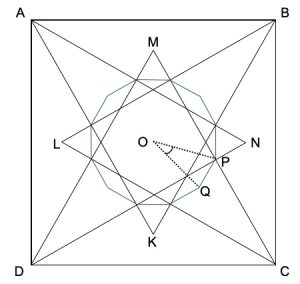

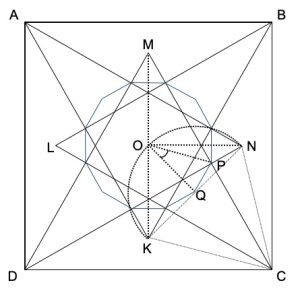
Iniziamo considerando con BK = BC e l’angolo KBC = 30°, quindi BCK è un triangolo isoscele con gli angoli BCK = BKC = 75° così l’angolo KCD = 15°, come mostrato in figura seguente. Per simmetria, rispetto all’asse AC, avremo l’angolo BCN = 15° e KCN = 90° – 15° – 15° = 60°. Ne segue che il triangolo CKN è equilatero poiché CK = CN. Ora entrambi i punti O e P sono i punti medi dei due lati del triangolo MKC, O è il punto medio di MK e P è il punto medio di MC, quindi il segmento OP è parallelo a CK e ha lunghezza ½ CK. Perciò l’angolo gli NOP = KCD = 15°. Ora tracciamo un semicerchio di diametro KN, con il centro in Q, per cui l’angolo KON è retto, quindi OQ = ½ KN = ½ CK = OP. L’angolo NOQ è di 45° e quindi l’angolo POQ = NOQ – NOP = 45° – 15° = 30° che è quello che volevamo dimostrare.

I Giochi del Lunedì di Prisma tornano tra due settimane.