129. Soluzioni del 12 agosto 2024 – Probabilità, cerchi e circonferenze

Le soluzioni del 12 agosto 2024 a cura di Fabio Ciuffoli

Ieri abbiamo presentato due giochi di geometria e calcolo delle probabilità e di seguito pubblichiamo le nostre proposte di soluzione.  

Probabilità, cerchi e circonferenze – soluzioni 

1. Qual è la probabilità di colpire a caso, all’interno di un cerchio, un punto più vicino al centro anziché alla circonferenza esterna? (I colpi fuori dal cerchio non sono conteggiati)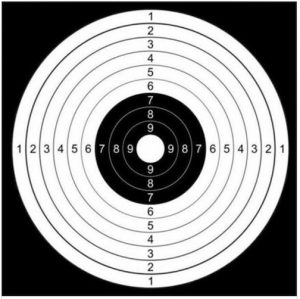

1. SOLUZIONE. Definendo r il raggio della circonferenza esterna, il punto colpito sarà più vicino al centro se è solo se sarà interno al cerchio di raggio r/2. L’area del cerchio grande è πr² e l’area del cerchio piccolo è π(r/2)² che diviene πr²/4. Il rapporto tra area piccola e area grande è quindi ¼ per cui la probabilità di colpire casualmente un punto più vicino al centro anziché alla circonferenza esterna è del 25%.

2. Prendendo due punti casuali su una circonferenza quante probabilità si hanno di avere una distanza tra di loro minore del raggio r?

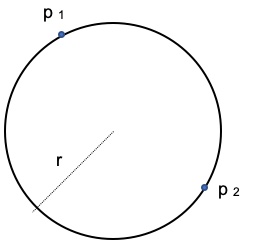
2. SOLUZIONE. Indicando con p₁ un punto qualsiasi sulla circonferenza, la condizione è soddisfatta se p_x cade sulla corda p₁ p_x di lunghezza inferiore al raggio r. Indicando con O il centro della circonferenza, tale corda è anche il lato di un triangolo equilatero p₁p_xO. L’angolo con vertice in O è di 60 gradi e la condizione sarà soddisfatta se p_x cade a destra o a sinistra di p₁, quindi la probabilità è 60×2/360=1/3 ossia il 33,33%. 

Alcuni hanno interpretato il testo, in modo impreciso, pensando che la distanza fosse sulla circonferenza e hanno considerato un arco di circonferenza anziché una corda. In questo caso il risultato sarebbe 2r/2πr che diviene 1/π uguale al 31,85%.

I Giochi del Lunedì tornano tra due settimane.