I Giochi del Lunedì di Prisma del 5 maggio 2025 a cura di Fabio Ciuffoli
Oggi proponiamo quattro problemi con coccinelle immaginarie, che si rincorrono a partire dai vertici di figure geometriche regolari. Si tratta, ovviamente, di un artificio che ci permetterà di ragionare sui metodi di soluzione di problemi geometrici più o meno complessi. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le nostre proposte di soluzione.
Coccinelle e poligoni regolari
Iniziamo con un esempio molto semplice. Se due coccinelle, collocate agli estremi di un segmento AB di lunghezza 1, partono nello stesso istante e si muovono l’una verso l’altra alla stessa velocità costante, si incontreranno a metà segmento e ciascuna avrà percorso ½ del segmento AB come schematizzato in figura. [In questo tipo di problemi le dimensioni della coccinella sono ininfluente]
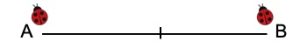
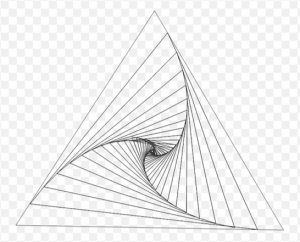
1. Immaginiamo tre coccinelle collocate ai rispettivi vertici di un triangolo equilatero di lato 1. Ogni coccinella inizia a muoversi verso la coccinella immediatamente vicina in senso orario. (Non importa se vanno in senso orario o antiorario). Le coccinelle partono nello stesso istante, corrono tutti alla stessa velocità costante e in ogni momento ogni coccinella corre direttamente verso la coccinella vicina. Durante l’inseguimento, le coccinelle corrono a spirale prima di incontrarsi tutte al centro, come schematizzato in figura. Quanto percorre ogni coccinella prima di incontrarsi con le altre?
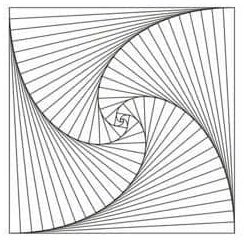
2. Quattro coccinelle sono ai quattro vertici di un quadrato di lato 1. Ogni coccinella inizia a correre verso la coccinella immediatamente vicina in senso antiorario. (Non importa se vanno in senso orario o antiorario). Le coccinelle partono alla stessa ora, corrono tutti alla stessa velocità e in ogni momento ogni coccinella corre direttamente verso la coccinella vicina. Durante l’inseguimento, le coccinelle corrono a spirale prima di incontrarsi tutte al centro, come schematizzato in figura. Quanto percorre ogni coccinella prima di incontrarsi con le altre?
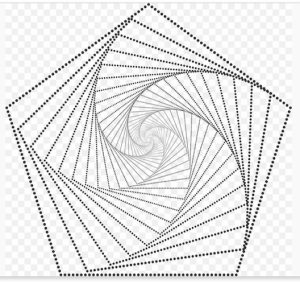
3. Cinque coccinelle sono ai cinque vertici di un pentagono regolare di lato 1. Ogni coccinella inizia a correre verso la coccinella immediatamente vicina in senso antiorario. (Non importa se vanno in senso orario o antiorario). Le coccinelle partono alla stessa ora, corrono tutti alla stessa velocità e in ogni momento ogni coccinella corre direttamente verso la coccinella vicina. Durante l’inseguimento, le coccinelle corrono a spirale prima di incontrarsi tutte al centro, come schematizzato in figura. Quanto percorre ogni coccinella prima di incontrarsi con le altre?
4. Sei coccinelle sono ai sei vertici di un esagono regolare di lato 1. Ogni coccinella inizia a correre verso la coccinella immediatamente vicina in senso antiorario. (Non importa se vanno in senso orario o antiorario). Le coccinelle partono alla stessa ora, corrono tutti alla stessa velocità e in ogni momento ogni coccinella corre direttamente verso la coccinella vicina. Durante l’inseguimento, le coccinelle corrono a spirale prima di incontrarsi tutte al centro, come schematizzato in figura. Quanto percorre ogni coccinella prima di incontrarsi con le altre?

Il problema delle coccinelle è stato trattato da vari autori di matematica divulgativa. La nostra esposizione ha preso spunto dal testo ‘Calculus made easy’ di Silvanus P. Thompson e di Martin Gardner.
Nell’immagine in evidenza “La passeggiata delle tre coccinelle” di John Rutherford Boyd.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
5 risposte
Una piccola correzione: il limite finale è di l_1-l_2 e non il contrario, ovviamente.
Se i conti sono giusti e non ho sbagliato a passare al limite il risultato per un n-gono regolare dovrebbe essere
S_n = 1/(1+cos(\pi*(n-2)/n))
Quindi S_3 = 2/3, S_4 = 1, S_5 = (3+sqrt(5))/5, S_6 = 2 e via dicendo.
Il conto si basa (in breve) sullo sfruttare che tale spirale S è proporzionale al lato l_1 del poligono in questione. A questo punto, dato un segmento x piccolo, si calcola il lato l_2 del poligono inscritto in quello iniziale tale che ogni suo vertice stacchi, in senso orario, sui lati del poligono iniziale segmenti di lunghezza x (usando il teorema di Carnot). Ora, sfruttando il fatto che S*l_1 = S*l_2 + x è un’approssimazione valida rettificando la spirale S, possiamo dire che S = lim(x->0+) di x/(l_2 – l_1).
Per ogni frazione x percorsa sul segmento ideale che unisce due coccinelle in un dato istante, rimane da percorrere una lunghezza pari a (Carnot) sqrt(x^2+(1-x)^2-2x(1-x)cos((n-2)PI/n)) dove n è il numero dei lati del poligono regolare in questione. Sommando tutti questi piccoli contributi si trova la lunghezza totale del percorso di ciascuna coccinella. Dapprima ho provato con Excel trovando valori abbastanza indicativi, poi sono riuscito a impostare il limite di una sommatoria in Wolfram che mi fornisce i seguenti valori:
Triangolo: 2/3
Quadrato: 1
Pentagono: ~1.44721
Esagono: 2
La formula è lim(x->0) della somma per k da 0 a inf di x*sqrt(x^2+(1-x)^2-2x*(1-x)*cosalpha)^k naturalmente impostando ogni volta il valore di cosalpha.
N. 1. Mi verrebbe, che ogni braccio della spirale è uguale alla lunghezza del lato 1m. percio’ 1 coccinella percorre 1 metro.
Problema 2, esattamente 1, a occhio…ma anche ragionandoci sopra