Ignorare la geometria fa male a tutti!

Prendo spunto da una questione poco rilevante per tornare su un argomento che ho più volte commentato in questi anni, e cioè quanto la geometria sia sempre più trascurata, per non dire ignorata, nell’insegnamento scolastico e quante deleterie conseguenze ciò comporti.

Il pretesto me l’ha fornito, sul numero 62 di Prisma, il problema “Un trapezio isoscele”, per il tour giochistico di Prisma; mi aveva stupito che fosse etichettato L1, cioè destinato ai ragazzi dal secondo all’ultimo anno della scuola secondaria di secondo grado. La soluzione balzava all’occhio, e il problema mi pareva quindi più adatto alla scuola primaria o semmai alle prime classi della scuola media. Ecco il testo:

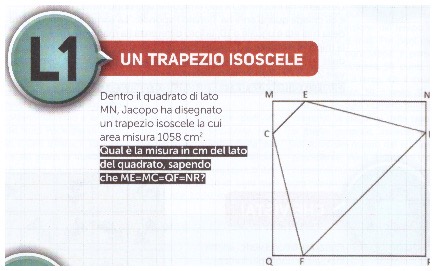
Sul numero 63 è poi comparsa la soluzione proposta da Prisma (che riportiamo qui sotto).

Che dire? Non mi stupisce più (per averlo già visto troppe volte!) che si usi il calcolo algebrico per giustificare qualunque minimo problema geometrico (qui davvero minimo: basta osservare che le diagonali del trapezio dividono il quadrato in 4 rettangoli, ciascuno diviso a sua volta dai lati del trapezio in due triangoli di uguale area; l’area del quadrato è quindi il doppio dell’area del trapezio). Mi stupisce però che, arrivando in fondo al calcolo algebrico, una volta che si è scoperto che l’area del quadrato è esattamente 2 volte l’area del trapezio (proprio 2, non 2,35 o 1,84…!), non sia nata la curiosità di capire come mai è proprio il doppio, se c’è una ragione geometrica che lo giustifica (e che resta nascosta dalla semplice esecuzione di un calcolo).

Ognuno, naturalmente, è libero di usare gli strumenti che gli sono più congeniali. Però una rivista come Prisma, che annovera fra i suoi lettori molti insegnanti, e di diversi livelli scolastici, dovrebbe tener conto anche del punto di vista didattico, in particolare quando propone giochi e problemi; e, da questo punto di vista, ci sono buoni motivi (qui sopra ne abbiamo visto già uno!) per preferire un’argomentazione geometrica al calcolo algebrico proposto nella soluzione di Prisma. Ma, soprattutto, la soluzione riportata manda implicitamente un messaggio in negativo agli insegnanti di scuola primaria e di scuola secondaria di primo grado: “Questo problema non è adatto ai vostri alunni”.

E questo invece non è proprio vero!

Per avere conferma di quest’ultima affermazione, ho chiesto la consulenza di qualche collega che insegna in questi ordini di scuola; la mia richiesta ha suscitato molto entusiasmo (da parte degli insegnanti e da parte dei bambini) e… sono sommersa dalle risposte! Già le prime che ho ricevuto (da classi di IV e V della scuola primaria e I della scuola secondaria di primo grado) sono sufficienti a confermare che il problema è proponibile a questo livello: tutti i ragazzi ci provano in maniera proficua, anche quelli non particolarmente “forti” in matematica; molti arrivano alla risposta corretta (e gli insegnanti ci fanno notare che non si tratta soltanto di qualche alunno isolato e particolarmente brillante), ed è bello vedere che i ragazzi ci arrivano da più strade differenti – alcune delle quali inaspettate! – e che il problema ha fatto emergere tanti utili collegamenti.

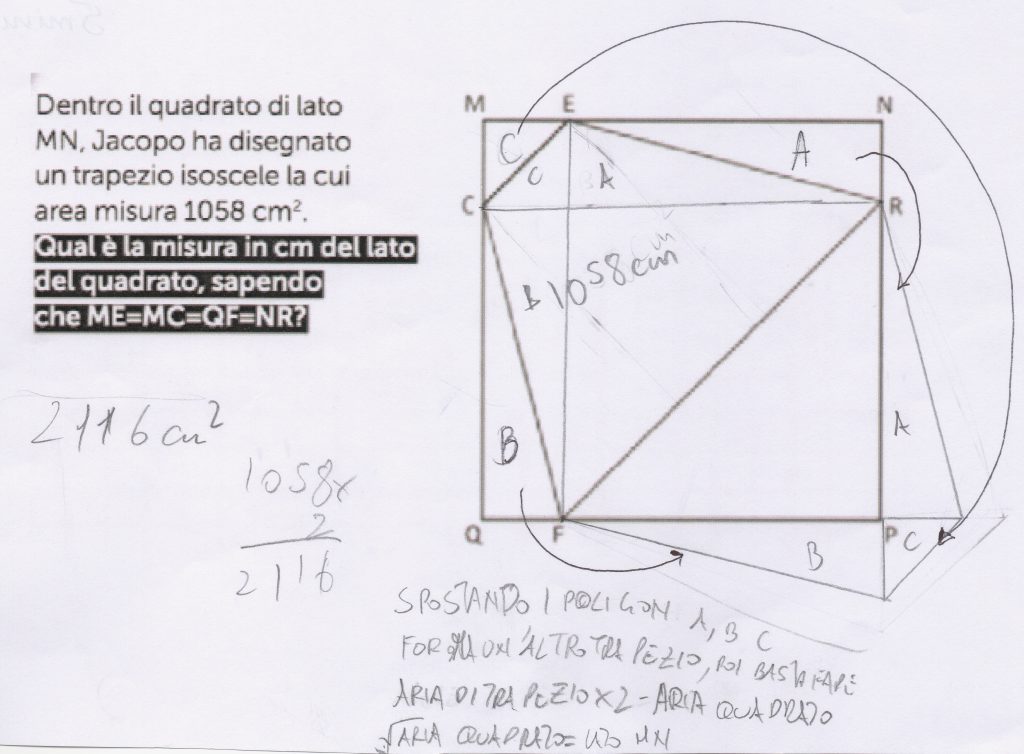
Ecco qui sopra una delle soluzioni, proposta da alunni di una I classe della secondaria di primo grado.

Qui sopra invece la soluzione, prima “sperimentata” e poi svolta in via teorica, proposta da una quarta elementare.

Ma usciamo dallo spunto offerto dal problema di Prisma. Anche sui libri scolastici non è raro incontrare situazioni analoghe, quando viene introdotto un nuovo strumento un po’ più sofisticato (succede per esempio col calcolo algebrico, ma anche con la geometria analitica e anche con altro) e poi si propone come esempio un problema che si può risolvere tranquillamente  “con le mani”, senza bisogno della nuova acquisizione.

Questo non è un bel biglietto da visita per il nuovo strumento che si sta introducendo: se i nostri alunni arrivano alla conclusione che in questo modo si risolvono in maniera più complicata (soltanto!) problemi che prima già sapevano fare in maniera più semplice, non hanno tutti i torti a concludere che la matematica non serve proprio a niente!