Matematica (quasi) senza numeri

È sempre così: che sia andato a mangiare una pizza o a farsi spennare in un ristorante stellato, che sia un tête-à-tête con una compagnia numerosa di amici, a cena, a pranzo o a colazione, c’è poco da fare: il matematico è, invariabilmente, colui al quale viene chiesto di dividere il conto. L’identificazione dell’abilità matematica con la capacità di far di conto è tanto diffusa da motivare la seguente dicitura, comparsa a più riprese sulla Settimana Enigmistica: “Basandosi solo sul ragionamento e cioè senza alcun ricorso alla matematica” (nella figura 1 un esempio).

Facciamo l’esegesi della frase: devo determinare un certo numero ma per farlo devo solo ragionare, ovvero NON ricorrere alla matematica. Ergo: “fare matematica” e “ragionare” sono due attività mutuamente esclusive. Fare matematica è dividere il conto al ristorante, ragionare è dare prova di intelligenza. E se lo dice La Settimana Enigmistica, che dal lontano 1932 costituisce il passatempo preferito di generazioni di lettori di tutte le età, è evidentemente spia del sentire comune. Se però guardiamo l’etimologia, che qualcosa vorrà pur dire, la parola matematica viene dal greco μάθημα (máthema) = scienza, conoscenza, apprendimento, e chi la pratica è quindi un μαθηματικός (mathematikós), “incline a conoscere”. Ora, diciamocelo, che cosa c’è di affascinante nel saper dividere il conto del ristorante? E perché persone “inclini a conoscere” dovrebbero voler perdere il loro tempo in operazioni di questo tipo che, una volta imparate, richiedono solo una buona abilità di riproduzione? Del resto, la diffusa identificazione del “bravo in matematica” come quello che risolve nel tempo più breve l’espressione più lunga è destinata a creare frustrazione se non al liceo, certamente all’approdo all’università. Quelli che ci riescono magari si divertono, quelli che invece hanno più difficoltà neppure quello. Per entrambe le categorie, questo tipo di attività ha comunque poco di creativo. È un buon allenamento della capacità riproduttiva di risolvere esercizi, ma con la matematica ha poco a che spartire. Questo perché, come Paul Halmos diceva in tempi non sospetti, l’attività chiave di chi fa matematica è “risolvere problemi”. Che non sono, naturalmente, esercizi mascherati (pure male), tipo il seguente: “Una pentola ha la forma di un prisma retto che ha per base un triangolo equilatero; il lato del triangolo è uguale all’altezza del prisma, che è uguale a un metro. Calcolare…”. Sorvoliamo. Quello che differenzia un problema da un esercizio non è (soltanto né soprattutto) la presenza di una struttura narrativa, possibilmente non incongrua, ma è la natura “produttiva” del compito proposto che richiede l’attivazione di un pensiero strategico e, quasi necessariamente, lo sbattere la faccia contro l’errore. Vi accorgete di star risolvendo un problema nel momento in cui sentite, nel vostro cervello, “le cellule grigie” – direbbe Poirot – che fanno cri-cri, cri-cri. E questo, va da sé, si può ottenere tranquillamente senza numeri. O, meglio, senza conti. Proprio come succede nell’esempio del problema (che tale è, e pure carino) proposto dalla Settimana Enigmistica, dove i numeri potrebbero tranquillamente essere sostituiti da simboli di qualsiasi genere perché non serve usarli per fare conti. Su questi quattro numeri si hanno i seguenti dati, tutti riferiti al numero esatto da trovare: in A ci sono tre cifre in posizione esatta e in B è errata la posizione di due sole cifre; in C solo una cifra è in posizione esatta mentre in D le cifre in posizione esatta sono quattro. Qual è il numero esatto? Prendete un foglio e provate a risolverlo: sapete fin dall’inizio come procedere? No. Commettete errori? Può essere. Le celluline grigie fanno cri-cri? Sì. Vi divertite? Molto. Ecco, state facendo matematica! Magari, però, tutte queste cifre vi disturbano, anche se non vi viene richiesto di combinarle per fare conti. Mettiamoci quindi alla prova con un enunciato in cui non ne compare nemmeno una. Guardate la figura 2 della pagina successiva: rappresenta un cavallino e uno strano recinto. Sapreste dire se il cavallino è dentro o fuori dal recinto?

Mettetevi buoni e provate: qualcuno di voi colorerà, qualcuno cercherà cammini… poi ciascuno di voi darà la sua risposta. Motivatela e poi cercate di capire se, con la stessa tecnica, sareste in grado di dare la risposta allo stesso problema, nel caso in cui il recinto fosse molto più complicato (pur restando un recinto ovvero una staccionata ininterrotta, senza aperture e che non si autointerseca). Chi ha colorato a un certo punto si ferma e anche a chi ha cercato un cammino… serve un’idea. Di quelle che, quando le trovate, vi chiedete come avete fatto a non vederle prima. Ecco: cercare l’insight, magari dopo aver accumulato tentativi ed errori, e poi verificare che sia proprio l’idea giusta… anche questo è fare matematica. Attenzione: non stiamo dicendo che la matematica sia tutta qui, né che sia un gioco, né che sia alla portata di chiunque. Anche un problema semplice come quello del cavallino, per esempio, dipende da proprietà profonde del piano e può decollare in complessità anche semplicemente cambiando la superficie su cui lo si propone. Immaginiamo che il povero cavallino abbia la scomodità di abitare sulla superficie di un nastro di Moebius o su un più comodo ma altrettanto inquietante toro (nome in codice con cui i matematici chiamano la ciambella). Si potrebbe ancora applicare lo stesso ragionamento? Perché sì o perché no? Rispondere a queste domande è a un livello diverso di complessità ed è, ancora una volta, fare matematica. In certi casi, problemi di questo tipo consentono anche ai non professionisti di intravedere la punta dell’iceberg di interi settori della matematica o di interi concetti che si sono rivelati molto fecondi in tutta la storia del pensiero matematico. Come quello di invariante, per esempio. Per presentarlo, utilizziamo un altro cavallo, stavolta quello degli scacchi, che si muove a L, due caselle in orizzontale o verticale più un’altra ad angolo retto con la prima. Partendo quindi per esempio dalla posizione che occupa nella figura 3, il cavallo può raggiungere con una mossa tutte le caselle indicate dalla punta di una delle frecce rosse. Ebbene: se parte dall’angolo in basso a sinistra, può arrivare a quello in alto a destra dopo aver toccato una e una sola volta tutte le altre caselle?

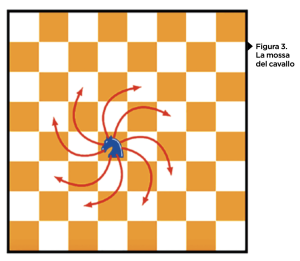
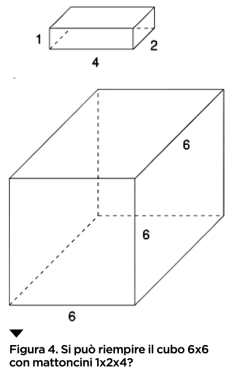
Di fronte a un problema di questo tipo, il primo approccio è rimboccarsi le maniche e procedere per tentativi. Provi, provi, provi … e non ti riesce! Dopo un po’ inizia a farsi strada l’idea che non si possa fare. Attenzione, però: potresti non avercela fatta perché sei scarso o perché non hai provato abbastanza! Per escluderlo, bisogna che tu trovi il modo di “dimostrare” che quel cavallo, da un angolo a quello opposto, non ci può andare. Vediamo un po’: guardando la figura 3, che cosa accomuna tutte le caselle indicate dalla punta delle frecce? Non leggere la risposta subito, aspetta almeno i primi cri-cri!!! Ok, siamo d’accordo: le accomuna il colore – se il cavallo parte da una casella arancione, con una mossa arriva in una casella bianca – e viceversa. Immaginiamo poi di aver scelto la prima mossa e di aver spostato quindi il cavallo della figura 3 in una delle caselle bianche indicate dalla punta di una freccia: che cosa accomuna, a questo punto, tutte le caselle nelle quali da lì può arrivare con una sola mossa – ovvero quelle su cui il cavallo della figura 3 può arrivare con due mosse? Benissimo: le accomuna il colore, che a questo punto sarà bianco. Portando avanti questo ragionamento, vi accorgerete che emerge una regolarità: le caselle su cui si può trovare il cavallo dopo un numero pari di mosse hanno lo stesso colore di quella da cui il cavallo è partito, mentre in quelle raggiungibili con un numero dispari di mosse il colore cambia. Ci sono quindi una situazione (che è dove sta il cavallo) e una trasformazione di questa situazione operata da una mossa. Il colore non cambia (ovvero è invariante) se la mossa ammissibile la facciamo un numero pari di volte. Se quindi il cavallo parte dalla casella in basso a sinistra, che è arancione, sicuramente non può arrivare nell’angolo opposto dopo un numero dispari di mosse, perché la casella in alto a destra è dello stesso colore (quindi rientra tra le caselle eventualmente raggiungibili solo in un numero pari di mosse). Perché questo vi porti a risolvere definitivamente il problema del cavallo lo lasciamo dire a voi lettori. Qui ci preme sottolineare come questo sia un esempio di come i matematici, a partire da un problemino apparentemente molto specifico, ragionano, generalizzano e rendono astratto un pacchetto di ragionamenti che a un certo punto non ha più nemmeno a che fare con il singolo problema di partenza. Adesso sappiamo che, se in una situazione che si trasforma nel tempo riconosciamo un qualcosa che rimane invariato per questa trasformazione, la configurazione iniziale e quella finale devono averlo entrambe. Se quella finale non ce l’ha, allora non è possibile arrivarci. Il che come principio astratto è estremamente fecondo e potente. Provate, per esempio, ad affrontare un esempio (molto) più difficile, in cui però si arriva alla soluzione applicando lo stesso principio. Stavolta prendiamo un bel cubo di lato 6, e lo vogliamo riempire con mattoncini di lego della forma 1x2x4, come nella figura sotto. Provo e riprovo, faccio il primo piano, faccio il secondo piano ma, al massimo, al terzo salta sempre fuori qualche buco cubico di lato 2… Sarebbe più facile spaccare in due un mattoncino e metterlo lì a tappare il buco, ma non si può. Sarà mica che anche questo problema non si può risolvere? Caccia all’invariante… Le soluzioni? Non ve le diamo, possiamo solo suggerirvi di andare a questo link https://youtu.be/REilCajHj08 e vedere il video. Anche perché, come diceva Ennio De Giorgi, “un bel problema ti fa compagnia, se ci pensi ogni tanto”.