Tutti i matematici amano Calvino: che combinazione!

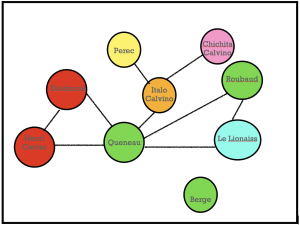
Nel 1967 Calvino si trasferisce a Parigi, dove cinque anni prima aveva conosciuto sua moglie, Esther, detta Chichita. Calvino sta traducendo I fiori blu di Raymond Queneau, uno scrittore francese che in quel periodo sta scrivendo un articolo di matematica pura sulle sequenze. Questo articolo sarà pubblicato nei Comptes rendus de l’Académie des Sciences de Paris, d’altra parte Queneau è invece membro della Societé mathématique de France che ha avuto come presidenti Henri Cartan e Jean Diodonné, fondatori del Gruppo Bourbaki. Bourbaki, pur non esistendo, portava al centro della matematica il metodo assiomatico e la teoria degli insiemi (dovremmo dire teoria degli insiemi e delle funzioni se fossimo interessati a relazioni tra gli insiemi, e qui ci aiuta Jacques Roubaud che  aveva scritto un bel lavoro riguardante le categorie ed era da poco entrato nel gruppo letterario Oulipo fondato da Queneau e François Le Lionnais). A questo gruppo letterario aderirono lo stesso Calvino e George Perec. Se vi siete persi a leggere queste righe, le schematizziamo mediante un grafo che è un insieme di punti e linee ben studiato da Claude Berge, anche lui membro di Oulipo. Forse troverete facilmente un significato alla colorazione del grafo (in rosso i matematici non membri di Oulipo, in rosa i non matematici e non membri di Oulipo, in verde i membri di Oulipo che hanno pubblicato un lavoro matematico, in giallo quelli che non l’hanno fatto e pubblicato solo letteratura, in celeste chi oltre la letteratura ha pubblicato storia, in arancione i letterati traduttori). Ma quale significato ho dato agli archi del grafo? È più difficile eppure è proprio sotto i vostri occhi.

La teoria dei grafi è una branca importante della combinatoria, parte della matematica a cui i membri di Oulipo si ispiravano. Calvino scrisse vari romanzi in cui esplicitamente vuole sperimentare il darsi una regola e seguirla fino in fondo. È l’assiomatica del romanzo, proprio come l’assiomatica della matematica. L’effetto della regola è un gioco serissimo in cui il lettore deve cercare la regola nascosta. Accettiamo l’invito.

Nelle Città invisibili, Marco Polo espone all’imperatore 55 città raggruppate in 11 tipologie

(Me) LE CITTÀ E LA MEMORIA;

(De) LE CITTÀ E IL DESIDERIO;

(Se) LE CITTÀ E I SEGNI;

(So) LE CITTÀ SOTTILI;

(Sc) LE CITTÀ E GLI SCAMBI;

(Oc) LE CITTÀ E GLI OCCHI;

(No) LE CITTÀ E IL NOME;

(Mo) LE CITTÀ E I MORTI;

(Ci) LE CITTÀ E IL CIELO;

(Co) LE CITTÀ CONTINUE;

(Na) LE CITTÀ NASCOSTE;

Il viaggiatore non si muove cercando città dello stesso tipo, ma chi racconta vuole un ordine. A leggere l’indice del libro questo ordine è nascosto. Come disporre le città? L’idea di Calvino è molto semplice: in verticale. Allora verrebbe un libro di 11 città di tipo diverso che si alternano? No, perché un libro sulle città deve essere un ordine tridimensionale e quindi ci devono essere dei gradini a dare profondità. Calvino mette l’elenco in verticale e costruisce una scala, poi crea l’indice leggendo la scala in orizzontale. C’è un altro modo di dare tridimensionalità.  Il numero 55 è un numero triangolare, possiamo mettere le città su 10 righe di un triangolo e poi osservare che 55=3*15+10, ovvero la somma di 4 numeri triangolari. Iniziamo mettendo i nomi delle città parallelamente tra loro sui lati dello sviluppo piano della piramide e chiudiamo il triangolo formando una piramide a base triangolare con facce laterali equilatere e congruenti.

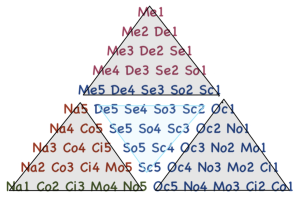
Quanto piacciono a Calvino i numeri triangolari! Ecco il piccolo numero 3 che in Palomar era usato creando la terna (vacanza, città, silenzio) ripetuta in nove trilogie così da avere 3^3 testi.

E il 6 delle due serie di storie ascoltate nel Castello e nella Taverna dei destini incrociati. Ma no, sono sette se ci aggiungiamo l’autore. Piano piano, confrontiamo questa questione con il 10, il successivo numero triangolare. Calvino in Se una notte d’inverno un viaggiatore scrive dieci incipit di dieci tipi di romanzo diversi ma che letti di seguito formano un undicesimo romanzo. E poi c’è la cornice, i lettori interni ed esterni dei dieci romanzi. La cornice è un altro romanzo, siamo a dodici, e l’autore mette una piccola indicazione nel testo a questo numero quando viene consegnata “una fune molto lunga: dieci, anzi dodici metri”. Ci sta dicendo che combinando si ha un numero maggiore. È così anche in matematica, da quattro elementi se ne hanno 24 e in generale da n se ne hanno n! Anche le carte dei tarocchi sono in numero triangolare, ovvero 78. Anche qui le storie sono raggruppate con un numero triangolare (sei nel castello e sei nella taverna). La combinatoria ci dice che ci sono 78! modi di disporre le carte, è un numero grandissimo, il punto di Calvino è la scelta. Come si sceglie un racconto? Qui ogni carta ha senso solo in relazione con la carta precedente e successiva. Non più elenco ma sequenza, che era l’oggetto dell’articolo matematico di Queneau di cui ho parlato all’inizio. Anche io ho chiuso il grafo, ho giocato come mi ha insegnato questo grande maestro del sapere.

PS. Nel grafo con cui si apre questo articolo sono connessi solo i soggetti che si trovano nel mio scritto nella stessa frase.