Laboratorio “Frazioni e dintorni”

4 Ottobre 2023
di AA.VV.

Questo percorso laboratoriale è stato proposto nell’ambito del Corso MathUp per la classe seconda della scuola secondaria di I grado dell’anno scolastico 2017/18; è stato elaborato da Paolo Lorenzi, docente del corso, Ilaria Criscuolo, Clara Lago e Elisabetta Meynet, tutor del corso, prendendo spunto da alcuni materiali presenti in rete:

http://repository.indire.it/repository/working/export/474/1537.htm

http://www.scuolavalore.indire.it/nuove_risorse/frazioni-in-movimento /

Struttura del percorso:

PRIMA SESSIONE

Attività 1 – Gioco “In ordine!”
Attività 2 – Costruzione e osservazione di due tabelle, una con le frazioni e una con i corrispondenti numeri decimali.

SECONDA SESSIONE

Attività 3 – Costruzione e osservazione di una tabella con i corrispondenti numeri misti
Attività 4 – Costruzione e osservazione di una tabella con le corrispondenti percentuali
Attività 5 – Il nucleo di una cometa

TERZA SESSIONE

Attività 6 – Riproposizione del gioco “In ordine!” (vedi Attività 1)

Attività 7 – Problemi di difficoltà variabile in cui è necessario passare da una rappresentazione dei numeri razionali all’altra.

PRIMA SESSIONE

ATTIVITÀ 1 – Gioco “In ordine!”

Obiettivi, processi e competenze in gioco:

eseguire confronti fra numeri conosciuti;
motivare gli alunni alla ricerca di tecniche via via più efficaci; imparare a imparare;
rafforzare le competenze relazionali e sociali.

Tempo 30’ – Attività di gruppo

Materiale

Regole del gioco

Tessere per il gioco distinte per tre livelli di difficoltà.

Esempio di gioco.

http://specchi.mat.unimi.it/users/specchi/matematica/secIgrado_ugualiodiversi_domino.html

Descrizione

Formiamo gruppi di 3 o 4 alunni in relazione alla numerosità della classe.

Consegniamo le tessere ai gruppi scegliendo il livello di difficoltà desiderato e giochiamo secondo le regole.

ATTIVITÀ 2 – Tabelle con frazioni e numeri decimali

Obiettivi, processi e competenze in gioco:

esprimere il rapporto fra due numeri sia nella forma decimale, sia mediante frazione;
utilizzare frazioni equivalenti e numeri decimali per denotare uno stesso numero razionale in diversi modi;
conoscere e padroneggiare diverse forme di rappresentazione di una frazione e saper passare da una all’altra (verbale, scritta, simbolica, grafica…);
approssimare il risultato di divisioni;
rappresentare insiemi di dati, anche facendo uso del foglio elettronico;
eseguire divisioni quando possibile a mente oppure utilizzando gli usuali algoritmi scritti, le calcolatrici e i fogli di calcolo;
osservare regolarità e generalizzare;
rafforzare le competenze relazionali e sociali.

Materiale

Scheda studente 1

Scheda studente 2

Scheda studente 2 bis

Tempo 70’ – Attività prima individuale e poi di gruppo

Descrizione

Proponiamo agli alunni di completare una tabella a doppia entrata che riporti nella prima colonna i numeri naturali da 1 a 5 (saranno il numeratore della frazione) e in prima riga analogamente i naturali da 1 a 5 (saranno il denominatore), così da trovare negli incroci la frazione di numeratore e denominatore dati dalla coppia ordinata (a, b). Per esempio, alla coppia (3,4) corrisponderà la frazione ¾. (Scheda studente 1)

Nella tabella successiva facciamo scrivere negli incroci i numeri decimali ottenuti dalla divisione tra numeratore e denominatore, fermandoci a due cifre dopo la virgola. Eseguire le divisioni a mano, senza l’ausilio di una calcolatrice, potrebbe essere l’occasione per fare un po’ di esercizio con il calcolo a mano e a mente. Inoltre l’attività offre lo spunto per riflettere sull’approssimazione e sui numeri decimali limitati e illimitati.

Per consolidare l’idea di frazione e per facilitare la formazione del concetto, collegandolo anche a una rappresentazione grafica, chiediamo di associare alcune immagini (rettangoli quadrettati o torte) alla relativa frazione. È il caso che si faccia riflettere frequentemente i ragazzi sulla rappresentazione grafica, che potrebbe avere interpretazioni ambigue come nel caso della figura formata da tre quadrati, ciascuno diviso in quattro parti uguali, delle quali, nel primo e nel secondo, sono colorate tutte e quattro, mentre nel terzo solo una (9/4 o 9/12?). Ciò che vogliamo dagli alunni è che individuino due interi e un quarto, quindi una rappresentazione grafica di 9/4. Potrebbe però succedere che qualcuno intenda la figura come rappresentazione della frazione 9/12 = 3/4. È necessario dedicare un po’ di tempo per discutere in classe su questa ambiguità e su quali sono le differenze tra le interpretazioni della figura.

A questo punto, i ragazzi, in gruppo, risponderanno alle domande guida, poste nella seconda parte della scheda 1. Le domande sono poste per condurre i ragazzi a riscoprire le caratteristiche dei numeri razionali (frazioni o decimali) che si trovano su, sopra o sotto la diagonale principale delle due tabelle proposte (sono uguali, minori o maggiori di uno, …, hanno il denominatore uguale, maggiore, minore del numeratore, …). Costruendo le tabelle e rispondendo alle domande, gli studenti prendono confidenza con la scrittura decimale e frazionaria di un numero razionale, fanno esperienza di frazioni uguali o maggiori dell’unità consolidando o modificando le rappresentazioni mentali precedenti.

Nella Scheda studente 2 proponiamo di ingrandire le tabelle e di rispondere a domande riguardanti le regolarità che si possono osservare. A seconda del tempo che decide di dedicare a questa attività, l’insegnante può scegliere se proporre le tabelle già pronte agli alunni, in formato cartaceo o su foglio elettronico, oppure se farle costruire ai ragazzi con il foglio di calcolo. Quest’ultima opzione richiede che i ragazzi abbiano già preso confidenza con il foglio di calcolo e con la copiatura delle formule. Trovate le istruzioni al riguardo nella Scheda studente 2-bis.

SECONDA SESSIONE

ATTIVITÀ 3 – Tabella con numeri misti

Obiettivi, processi e competenze in gioco:

osservare, classificare e rappresentare uno stesso numero razionale in diversi modi, prendendo consapevolezza di vantaggi e svantaggi delle diverse rappresentazioni. Passare da una rappresentazione all’altra;
rappresentare insiemi di dati, anche facendo uso del foglio elettronico;
osservare regolarità e generalizzar;
rafforzare le competenze relazionali e sociali.

Tempo 25’ – Attività di gruppo

Materiale

Scheda studente 3

Descrizione

Nella tabella 3 proponiamo ai ragazzi la tabella già vista, ma con notazione anglosassone.

L’obiettivo è di far riflettere sulle frazioni che rappresentano quantità maggiori di un intero. Partendo dalle osservazioni su una casella corrispondente nelle diverse tabelle, si portano i ragazzi a dare significato alla scrittura anglosassone e a capire come si può passare da una scrittura all’altra.

La scelta di formulare alcune domande su una sola casella (cella) è dovuta alla necessità di dare indicazioni precise, ma sarà bene fare molta attenzione che questo non favorisca nei ragazzi l’idea che, trovata una regola per un caso, questa valga per tutti. Li dovremo far riflettere anche nel commentare il lavoro a laboratorio ultimato.

ATTIVITÀ 4 – Tabella con le percentuali

Obiettivi, processi e competenze in gioco:

osservare, classificare e rappresentare uno stesso numero razionale in diversi modi, prendendo consapevolezza di vantaggi e svantaggi delle diverse rappresentazioni. Passare da una rappresentazione all’altra;
comprendere il significato di percentuale e saperla calcolare utilizzando strategie diverse;
rappresentare insiemi di dati, anche facendo uso del foglio elettronico;
osservare regolarità e generalizzare;
rafforzare le competenze relazionali e sociali.

Tempo 25’ – Attività di gruppo

Materiale

Scheda studente 4

Descrizione

Nella tabella 4 passiamo alle percentuali: se si dispone già del foglio di calcolo con le tabelle 1, 2 e 3, a questo punto la costruzione della tabella 4 diventa più veloce, altrimenti consegniamo la tabella 4 completata.

L’obiettivo è di far notare la possibilità di scrivere le stesse frazioni e i numeri decimali sotto forma di percentuali proponendo osservazioni analoghe alle precedenti.

Si propone poi un esercizio per il passaggio da una scrittura all’altra dei numeri razionali, con una riflessione sulle tecniche utilizzate.

ATTIVITÀ 5 – Il nucleo di una cometa

Obiettivi, processi e competenze in gioco:

denotare uno stesso numero razionale in diversi modi, prendendo consapevolezza di vantaggi e svantaggi delle diverse rappresentazioni;
passare da una rappresentazione all’altra;
saper calcolare una percentuale utilizzando strategie diverse;
sviluppare, oltre alle competenze matematiche, anche quelle scientifiche e tecnologiche;
capire come gli strumenti matematici appresi siano utili in molte situazioni della realtà;
rafforzare le competenze relazionali e sociali.

Tempo 50’ – Attività di gruppo

Materiale

Scheda studente 5

Descrizione

Proponiamo la scheda 5, nella quale viene riportata una tabella che descrive la composizione del nucleo di una cometa. In questa attività si chiede innanzitutto di trasformare alcuni numeri decimali in percentuali e si introduce il concetto un po’ ostico della percentuale di percentuale.

Questa attività è stata scelta perché in quell’anno si erano trattati in scienze argomenti collegati a questo; naturalmente, a seconda degli argomenti trattati nei diversi anni, l’insegnante potrà scegliere problemi analoghi a questo dal punto di vista della matematica coinvolta e che prendano spunto, invece che dal nucleo delle comete, dagli argomenti che (in quell’anno e in quella classe) si stanno trattando in scienze, in modo da aumentare gli stimoli e le motivazioni per gli alunni.

TERZA SESSIONE

ATTIVITÀ 6 – Gioco “In ordine!”

Obiettivi, processi e competenze in gioco:

eseguire confronti tra numeri conosciuti;
applicare nuove tecniche e verificare la loro efficacia; imparare a imparare;
rafforzare le competenze relazionali e sociali.

Tempo 30’ – Attività di gruppo

Materiale (cfr. Attività 1)

Regole del gioco

Tessere per il gioco distinte per tre livelli di difficoltà.

Esempio di gioco.

Descrizione

Riproposizione del gioco iniziale per verificare eventuali miglioramenti o il persistere di alcune difficoltà nell’individuare se una frazione sia maggiore, minore o uguale di altre e collocarla sulla retta nella posizione relativa ad altri numeri dati.

ATTIVITÀ 7 – Problemi

Obiettivi, processi e competenze in gioco:

individuare e collegare le informazioni utili, confrontare strategie di soluzione, esporre il procedimento risolutivo;
confrontare procedimenti diversi e produrre formalizzazioni che consentono di passare da un problema specifico a una classe di problemi;
autovalutazione (imparare a imparare);
capire come gli strumenti matematici appresi siano utili in molte situazioni della realtà;
rafforzare le competenze relazionali e sociali.

Materiale

Scheda studente 6

Tempo 100’ – Attività di gruppo

Descrizione

Si propongono dei problemi in cui è necessario applicare quanto osservato precedentemente. Nei testi sono presenti dati relativi (frazioni, percentuali…) e numeri assoluti; gli alunni devono dunque imparare a distinguerli e a collegarli.

I problemi sono di difficoltà diversa a seconda dei numeri presenti nel testo: il primo è più immediato, il secondo richiede una maggiore consapevolezza nel passaggio da numero decimale a frazione a percentuale.

Si richiede inoltre di inventare un problema analogo, in cui bisogna trovare l’intero conoscendone una parte data in valore assoluto e della quale si debba ricavare quale parte (frazione o decimale) dell’intero essa sia. Questo è un utile strumento di autovalutazione per lo studente e un buon indicatore di apprendimento per l’insegnante.

Scheda studente 1

Prima parte – Lavoro individuale

A. La Tabella 1 è costruita in modo che negli incroci si trovino le frazioni che hanno per numeratore il numero naturale che si trova nella prima casella della riga e per denominatore il numero naturale che si trova nella prima casella della colonna. Per esempio, 4/5 è nella casella che sta all’incrocio della riga che comincia con 4 e della colonna che comincia con 5.

Alcune frazioni sono già scritte. Ti chiediamo di completare la tabella.

Tabella 1

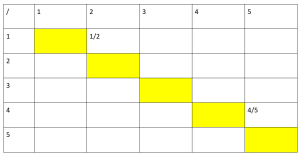
B. Completa la tabella 2 seguente scrivendo negli incroci il risultato della divisione tra numeratore e denominatore delle frazioni della tabella precedente.

Tabella 2

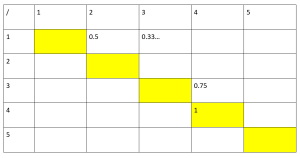
Ti proponiamo alcune rappresentazioni grafiche. Sotto la figura, dove ci sono i puntini, scrivi la frazione e il numero decimale che la figura rappresenta. Puoi aiutarti con le tabelle che hai appena completato.

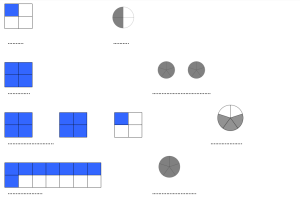
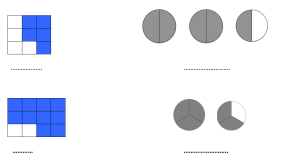
Seconda parte – Lavoro di gruppo

1. Osservate le tabelle e rispondete alle domande:

nella diagonale principale delle tabelle, individuata dalle caselle gialle:

che cosa hanno in comune le frazioni? _____________________________________________

e le rappresentazioni grafiche? __________________________________________________

quale/i numero/i trovate? _____________________________________________________

Immaginate di ingrandire una tabella a dimensione 100×100.In quali altre caselle siete sicuri di trovare la stessa situazione? _________________________________________________________

Perché? _______________________________________________________________________

_______________________________________________________________________

2. Osservate la metà tabella che sta SOPRA la diagonale principale:

che cosa hanno in comune le frazioni in queste caselle? _________________________________

e i numeri corrispondenti? _____________________________________________________

e le rappresentazioni grafiche? __________________________________________________

3. Osservate la metà tabella che sta SOTTO la diagonale principale:

che cosa hanno in comune le frazioni in queste caselle? _________________________________

e i numeri corrispondenti? _____________________________________________________

e le rappresentazioni grafiche? __________________________________________________

4. Immaginate di ingrandire la tabella:

scrivete tre frazioni che sicuramente si trovano SOPRA la diagonale principale

_______________________________________________________________________

scrivete tre frazioni che sicuramente si trovano SOTTO la diagonale principale

_______________________________________________________________________

spiegate il vostro ragionamento _______________________________________________________________________

_______________________________________________________________________

Scheda studente 2

Riportiamo le tabelle che avete costruito autonomamente estese fino alla riga e colonna dell’8.

Tabella 1

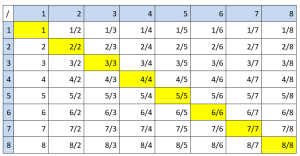
Tabella 2

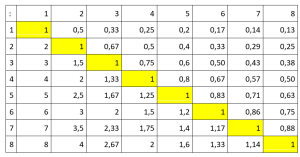
Lavoro di gruppo

Osservate le tabelle e rispondete alle domande.

1. Alcune caselle contengono un numero intero (per esempio, tutte quelle gialle contengono 1 o una frazione che lo rappresenta, ma ce ne sono anche altre, cercatene qualcuna); sapete distinguere quali caselle e perché, a partire dai due numeri che caratterizzano l’incrocio?

_______________________________________________________________________

2. Che cos’hanno in comune le rappresentazioni grafiche corrispondenti a queste caselle?

_______________________________________________________________________

3. Sapete prevedere se, continuando la tabella, il numero nella casella all’incrocio tra la riga del 35 e la colonna del 7 sarà intero oppure no? Perché?

_______________________________________________________________________

4. Osservate la tabella 2; ci sono dei numeri interi che compaiono in maniera regolare. Nella colonna del 2, si alternano (uno sì e uno no), nella colonna del 3 (due non sono interi e uno lo è, due no e uno sì, …): ma continuerà sempre così? Perché?

_______________________________________________________________________

5. Anche i numeri non interi hanno la parte decimale che si ripete in modo regolare: nella colonna del 3, per esempio, __,33 poi __,67 poi un intero poi ancora __,33 e continua a ripetersi. Continuerà anche andando oltre, con una tabella più grande? Riuscite a osservare fenomeni analoghi nelle altre colonne?

_______________________________________________________________________

6. Osservate i numeri decimali che stanno nella casella immediatamente sotto a una delle caselle gialle sulla diagonale. Per esempio, nella colonna del 4, trovate 1,25. Osservate che questo 1,25 è la somma del numero 1 nella casella gialla e del numero che trovate all’incrocio della stessa colonna e della riga che comincia con 1.
Sarà una coincidenza? Vedete nella tabella degli altri esempi? Immaginate che si ritrovi lo stesso fenomeno anche continuando la tabella? Sapete dare delle motivazioni di questo fenomeno?

_______________________________________________________________________

Scheda studente 2-bis

Utilizzando un foglio di calcolo si possono costruire automaticamente le tabelle 1 e 2 con le frazioni e i numeri e quindi estenderle molto velocemente.

COSTRUISCILE TU:

imposta le intestazioni di riga e colonna con i numeri dall’1 al 10;
per chiarezza, separa la riga e la colonna dell’intestazione con un bordo; puoi anche colorare le caselle dell’intestazione;
nella prima casella della tabella, inserisci la formula necessaria per il calcolo, per esempio =A2/B1.
trascina la formula nelle altre caselle;

ATTENZIONE: è necessario BLOCCARE LA RIGA 1 E LA COLONNA A usando il simbolo $;
per esempio =$A2/B$1. Generalmente dovrebbe comparire un numero decimale.

Per costruire la tabella con le frazioni, seleziona le caselle della tabella, scegli FORMATO/NUMERI/ALTRI FORMATI e cerca il formato “frazione”;
per costruire la tabella con i numeri decimali, seleziona le caselle della tabella, scegli FORMATO/NUMERI/NUMERO; puoi regolare il numero di cifre decimali;
prova a estendere le tabelle a tuo piacimento.

Scheda studente 3

Ora osserviamo e discutiamo la tabella 3. È stata compilata scrivendo le frazioni nel modo conosciuto come “scrittura anglosassone”.

Tabella 3

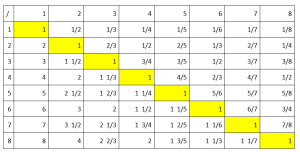
Lavoro di gruppo

Osservate le tabelle e rispondete alle domande:

1. Come è scritta la frazione posta nella posizione (7,3)? _________________________________

2. Confrontatela con la casella (7,3) di tab 1 e di tab 2, considerando anche le rappresentazioni grafiche. Cosa osservate?

_______________________________________________________________________

3. Date una spiegazione del significato della scrittura 2 1/3

_______________________________________________________________________

4. Scrivete la frazione che in un’estensione della Tabella 3, si trova nella posizione (25, 7).

_______________________________________________________________________

______________________________________________________________________

5. Come spiegheresti il passaggio alla scrittura anglosassone a un tuo compagno di quinta elementare?

_______________________________________________________________________

Scheda studente 4

Utilizzando un foglio elettronico si può automaticamente trasformare la tabella 1 (frazioni) in tabella 2 (numeri decimali), in tabella 3 (anglosassone) ma anche nella tabella 4 (percentuali) che riportiamo sotto.

Tabella 3

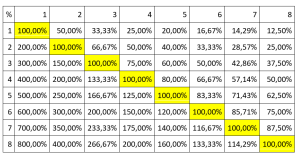
Lavoro di gruppo

Osservate le tabelle e rispondete alle domande:

1. Confrontate la casella (7,4) in ciascuna delle quattro tabelle. Si osserva che 7/4 si può scrivere come: _________________ _________________ _________________

2. Completate il seguente prospetto seguendo l’esempio riportato nella prima riga.

frazione	scrittura anglosassone	numero decimale	percentuale
3/5	3/5	0,6	60%
		1,4
			350%
25/7
	3 5/8
	2 3/4
			87,71%

3. Scrivete un breve messaggio per un vostro compagno assente alla lezione per spiegargli come scrivere i numeri passando da una tabella ad un’altra.

_______________________________________________________________________

Scheda studente 5

Come è fatto il nucleo di una cometa?

Ecco a voi ora un problema spaziale!

Il nucleo di una cometa, secondo alcuni studiosi, è composto da ghiaccio disseminato di rocce e particelle di polvere. Si tratta di un ghiaccio un po’ particolare, perché non è composto soltanto d’acqua.

Leggiamo questa breve presentazione, ricavata dal testo di A. Carbognani, Un Cielo Pieno di Comete, Gruppo B, 2014, e vediamo da che cosa è composto il nucleo nella tabella che segue.

3.4 Il nucleo

Riprendiamo il modello di Wipple e vediamolo più in dettaglio. Abbiamo detto che il nucleo consiste di una matrice di ghiacci disseminata di rocce e particelle di polvere, un vero e proprio conglomerato. Si stima che la parte ghiacciata costituisca l’80% della massa del nucleo. La composizione chimica (stimata), dei ghiacci presenti nel nucleo di una cometa è mostrata in Tabella 2.

Molecola	Abbondanza

H₂O (acqua)	0,85
CO (monossido di carbonio)	0,04
CO₂(biossido di carbonio)	0,03
H₂CO (formaldeide)	0,02
CH₃OH (metanolo)	0,02
N₂(azoto)	0,01
Altre	0,03
TOTALE

(tratto dal testo: A. Carbognani, Un Cielo Pieno di Comete, Gruppo B, 2014)

Calcolate la somma dei numeri che trovate nella colonna “Abbondanza” e scrivetela in corrispondenza del TOTALE . Date una spiegazione del perché di questo risultato.

_______________________________________________________________________

Che cosa significa ciascun numero decimale?

_______________________________________________________________________

Scrivete accanto a ciascun numero decimale la percentuale della massa di ghiaccio che rappresenta.

Quale percentuale della massa del nucleo è formata da acqua (H₂O) e quale da azoto(N₂)?

Acqua (H₂O)________% Azoto (N₂) ________%

Scheda studente 6

Problema: I LIBRI DELLA BIBLIOTECA

Oggi Lara e la sua compagna di banco sono state incaricate di restituire alla biblioteca della scuola tutti i libri che sono nell’armadio, perché ormai non c’è più spazio e alcuni ragazzi vogliono prendere altri libri.
Le due ragazze, visto che speravano di farsi aiutare dai compagni, hanno diviso i libri in 5 pacchi uguali.
Ma a quel punto l’insegnante ha chiesto loro di cominciare portando in biblioteca il 40% dei libri e di impegnarsi a portarne altri 2/5 (di quelli che erano nell’armadio all’inizio) il giorno dopo. In questo modo, avrebbe portato via lei gli 11 libri rimasti.

Quanti erano in tutto i libri da portare in biblioteca?

Quanti ne dovranno trasportare il giorno dopo le due ragazze?

Spiegate come avete fatto a dare la risposta.

Problema: LE ELEZIONI

Nella scuola di Alberto si sono appena svolte le elezioni per i rappresentanti degli alunni al consiglio di istituto.

Si sono presentate tre liste di candidati: “W la scuola”, “La scuola siamo noi”, “Andiamo a scuola”.

Dopo le elezioni gli alunni analizzano i risultati e scoprono che:

la lista “W la scuola” ha ottenuto 247 voti, la lista “La scuola siamo noi” ha ottenuto i 27/72 dei voti validi, la lista “Andiamo a scuola” ha ottenuto il 30% dei voti validi. 38 schede erano bianche e 19 nulle.

Nella scuola di Beatrice, le stesse tre liste hanno ottenuto i seguenti risultati: la lista “W la scuola” 228 voti, la lista “la scuola siamo noi” il 20% dei voti validi, la lista “andiamo a scuola” i 19/95 dei voti validi. Nessuna scheda era nulla, 19 schede erano bianche.

Alberto sostiene che la sua lista preferita, “W la scuola”, è andata meglio nella sua scuola, 247 voti contro 228, e che ha vinto le elezioni. Beatrice, però, non è convinta. Prende la calcolatrice e dopo aver fatto alcuni calcoli afferma: “Mi spiace contraddirti, ma “W la scuola” ha vinto le elezioni solo da noi!”

Secondo voi, chi ha ragione? Chi ha vinto nella scuola di Beatrice? E nella scuola di Alberto? Quanti voti ha ricevuto ciascuna lista nelle due scuole? Quanti studenti hanno votato in ogni scuola?

Aiutate i due amici ad interpretare i dati.

Lavoro di gruppo

Per entrambi i problemi, rispondete alle domande e motivate le risposte.
Costruite un problema simile utilizzando frazioni e percentuali (si possono utilizzare le tabelle che abbiamo costruito).

Laboratorio “Frazioni e dintorni”

Lascia un commento Annulla risposta