Non sembra, ma rimane uguale

Poniamo che si debba andare, sul piano, da un punto A verso un punto B.

Ci si può muovere prima in orizzontale e poi in verticale, così:

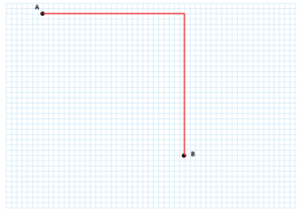
In questo modo la strada percorsa è di 27 quadretti verso destra e 27 quadretti verso il basso, per un totale di 54 quadretti. Si vede a occhio che non si tratta della strada più breve.
Si può provare quindi a percorrere un tragitto un po’ più diretto, come ad esempio il seguente:

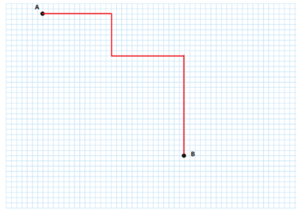
A prima vista la strada percorsa sembra più breve che nel caso precedente. In realtà, non è vero. Nonostante si cambi direzione varie volte, il numero di quadretti totale sia in orizzontale che in verticale rimane invariato (27) poiché se ne percorrono prima 13 in orizzontale, poi 8 in verticale, quindi altri 14 in orizzontale e infine 19 in verticale (13+14=27 e 8 +19=27).

Cambiando direzione un numero maggiore di volte si ottiene di frammentare ulteriormente i tratti in orizzontale e verticale.

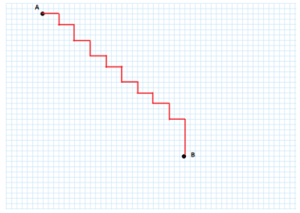
Agli effetti della strada totale percorsa, non si ha però alcun cambiamento. Per quanto riguarda i 9 tratti orizzontali le distanze coperte saranno rispettivamente di 3+3+3+3+3+3+3+3+3=27 quadretti. I 9 tratti orizzontali saranno di 2+3+3+2+3+2+2+3+7=27 quadretti.

Andando ad effettuare un numero ancora maggiore di cambi di direzione, si ottiene il seguente andamento:

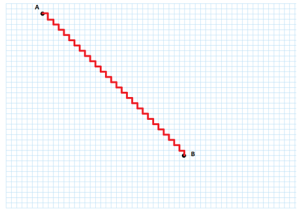
In questo caso si percorrono 27 tratti orizzontali da 1 quadretto e 27 tratti verticali da 1 quadretto. La distanza totale percorsa rimane quindi invariata. Generalizzando il procedimento, se dividiamo il tragitto orizzontale di 27 quadretti da percorrere in n parti, possiamo scrivere  dove a_i indica la lunghezza dell’i-esimo tratto orizzontale. In modo analogo, considerando che il numero di parti in cui suddividere il tragitto verticale deve essere necessariamente anch’esso pari a n, possiamo scrivere       dove b_i indica la lunghezza dell’i-esimo tratto verticale. Aumentare il numero di tratti porta a compiere un tragitto che assomiglia sempre di più a una traiettoria rettilinea tra i punti A e B, ma non abbrevia comunque la distanza da percorrere.

Se invece si ipotizza di muoversi in diagonale il tragitto percorso è il seguente:

In questo caso si percorrono 27 tratti orizzontali da 1 quadretto e 27 tratti verticali da 1 quadretto. La distanza totale percorsa rimane quindi invariata. Generalizzando il procedimento, se dividiamo il tragitto orizzontale di 27 quadretti da percorrere in n parti, possiamo scrivere  dove a_i indica la lunghezza dell’i-esimo tratto orizzontale. In modo analogo, considerando che il numero di parti in cui suddividere il tragitto verticale deve essere necessariamente anch’esso pari a n, possiamo scrivere dove b_i indica la lunghezza dell’i-esimo tratto verticale. Aumentare il numero di tratti porta a compiere un tragitto che assomiglia sempre di più a una traiettoria rettilinea tra i punti A e B, ma non abbrevia comunque la distanza da percorrere.

Se invece si ipotizza di muoversi in diagonale il tragitto percorso è il seguente:

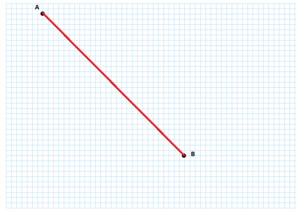
La distanza percorsa si trova con il teorema di Pitagora. La diagonale di un triangolo rettangolo isoscele di cateto 27 quadretti è √(27²+27²) cioè 27√2 che è circa 37,8 quadretti, cioè significativamente meno dei 54 quadretti che si percorrono andando in orizzontale e verticale. Tutto ciò in accordo con il noto teorema della disuguaglianza triangolare il quale afferma che, in un triangolo non degenere, la somma di due qualsiasi lati è sempre maggiore del terzo lato. Quindi in un triangolo rettangolo l’ipotenusa è sempre minore della somma dei due cateti.