Il diagramma dietro le reti wireless

Che cosa hanno in comune una giraffa, una libellula, una foglia, un parabrezza ghiacciato e un terreno arido? È una domanda che spinge a curiosare tra le immagini del web. Alcune forme geometriche, pur nella loro apparente deterministica casualità, sembrano ripetersi: dal manto delle giraffe alle ali delle libellule, dalle venature delle foglie ai cristalli di ghiaccio e alle crepe dei terreni aridi. In matematica queste forme possono essere modellizzate, cioè descritte in maniera semplificata, con le tassellazioni (o diagrammi) di Voronoi. Per capire che cosa sono, nel piano, vediamo un esempio che, ancora una volta, ci porta in un contesto diverso e lontano dai precedenti.

Immaginiamo di dover decidere noi dove un operatore telefonico debba posizionare dei ripetitori sul territorio, che chiamiamo generatori. Verosimilmente non potremo posizionare i ripetitori ovunque poiché dovremo rispettare vincoli architettonici, paesaggistici e logistici. Per valutare l’efficacia di un potenziale sito per un nostro ripetitore, saremo interessati a capire quale sia la sua “zona di competenza”, che chiameremo anche cella, che risponde a un principio di vicinanza; per capirci, un telefono cellulare si collega al ripetitore più vicino e tutti i punti dai quali si collega allo stesso ripetitore identificano la cella. Se ci stacchiamo dall’esempio, possiamo dire in termini più formali che la cella associata a un generatore è l’insieme dei punti che distano da quel generatore meno che da ogni altro generatore. Ora, per quanto elegante, la precedente caratterizzazione non risponde alla domanda: quale forma geometrica assume la singola cella? Può essere un triangolo? Un quadrato? Un cerchio? Per fornire una risposta, e apprezzare alcune proprietà della tassellazione di Voronoi, proviamo a considerare i casi più semplici e cioè con pochi generatori. Se il nostro operatore telefonico posiziona un solo ripetitore, tutti i cellulari gli si agganciano e la cella associata coincide con tutto il piano.
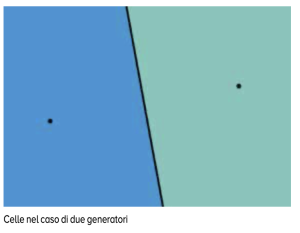
Se aggiungiamo un secondo ripetitore, il principio di maggior vicinanza crea indecisione se il telefono cellulare è alla stessa distanza dai due ripetitori. Tutti i punti equidistanti dai due generatori sono punti di “confine” tra le celle associate ai due generatori e stanno sull’asse del segmento che congiunge i due generatori (cioè sulla retta perpendicolare al segmento che passa per il suo punto medio). Questo asse viene chiamato in gergo matematico lato della cella ed è tale da separare le celle che contengono i due generatori. Nel caso dei due generatori, le celle a loro associate coincidono con i due semipiani divisi dal lato comune e un cellulare si collegherà a un ripetitore piuttosto che all’altro a seconda della sua posizione rispetto al lato tra le due celle. Aggiungendo un terzo generatore (cioè un nuovo ripetitore) non allineato con i precedenti, per identificare le celle associate a tutti e tre i generatori bisognerà tener conto di tutti i possibili segmenti che si possono formare tra coppie di generatori, quindi considerarne gli assi e infine identificare la cella corrispondente a ciascun generatore.

Avendo tre generatori avremo tre segmenti, altrettanti assi che si incontrano in quel punto che a scuola abbiamo imparato a chiamare circocentro del triangolo con i vertici dati dai tre generatori e che qui invece chiamiamo direttamente vertice del diagramma.

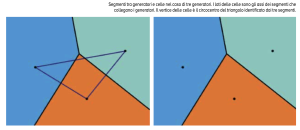
Aggiungendo via via nuovi generatori si dovrà considerare un numero sempre maggiore di segmenti, assi, vertici e semipiani per identificare le celle di ciascun generatore. In generale, le celle risultanti sono regioni convesse in quanto ottenute dall’intersezione di un numero finito di semipiani e possono essere limitate (e quindi sono poligoni convessi) oppure illimitate e ciò si verifica in corrispondenza dei generatori situati “più esternamente” (cioè quelli che si trovano ai vertici del più piccolo poligono convesso contenente tutti i generatori). Il lato di due celle adiacenti sarà parte dell’asse del segmento che collega i generatori delle celle considerate, mentre il vertice di tre o più celle sarà il centro di una circonferenza passante per i generatori associati alle celle che lo condividono. Si può dimostrare che il centro della circonferenza passante per tre generatori è un vertice della tassellazione se e solo se non contiene altri generatori al suo interno.

Quest’ultima proprietà è fondamentale soprattutto all’atto pratico, quando si vuol costruire il diagramma di Voronoi associato a un insieme finito di generatori, perché fornisce un criterio per individuare tutti i vertici della tassellazione. Basta infatti verificare se, data una terna di generatori non allineati, la circonferenza che passa per i tre punti non contenga altri generatori.

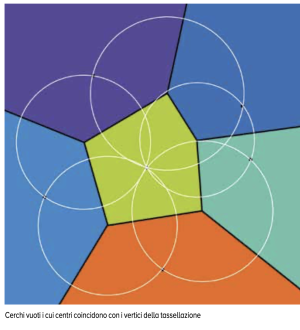
In questo caso, il suo centro sarà un vertice della tassellazione, altrimenti si passa a considerare un’altra terna di generatori non allineati e si ripropone la stessa domanda fintanto che non sono state esplorate tutte le possibili terne di generatori non allineati. In questa maniera si otterranno i vertici del diagramma e si verrà a sapere a quali lati e celle tali vertici appartengono, definendo quindi in maniera esplicita tutti gli elementi della tassellazione.

Questo metodo di costruzione del diagramma di Voronoi è detto delle “sfere vuote” (per il fatto che lo stesso ragionamento può essere generalizzato anche a uno spazio con dimensione maggiore) ed è stato descritto per la prima volta dal matematico sovietico Boris Delaunay al quale si devono diversi studi sulla tassellazione di Voronoi.