Il gioco era un azzardo anche nei secoli bui

Lanciare tre dadi e dichiarare a voce alta, prima del tiro, quale sarebbe stato il risultato della somma dei punti: la zara era il passatempo preferito nell’Italia del Medioevo. Il cruccio dei giocatori era indovinare le combinazioni più frequenti. Procedevano per tentativi perché la teoria della probabilità nascerà solo nella seconda metà del Seicento

Il Medioevo è stato un periodo di guerre e conquiste. Molte furono quelle di religione come le crociate, altre scoppiarono per la conquista di territori. Nonostante tutto, ci fu una particolare predisposizione per il gioco con numerosi momenti di svago e divertimento. Molto comune era il gioco degli scacchi che, nel movimento dei pezzi, ricorda una battaglia tra due eserciti. Erano comunque ben distinti i giochi di abilità, come gli scacchi appunto, nei quali la situazione di gioco dipende dalle scelte compiute dai giocatori, da quelli di abilità e fortuna come le “tavole” (per esempio il backgammon) e da quelli d’azzardo, dove è solo la fortuna del giocatore a stabilire il risultato della partita.
Questi giochi, illustrati con numerose miniature, sono descritti nel celebre El Libro de los Juegos commissionato da Alfonso X, re di Castiglia, León e Galizia e pubblicato nel 1283.
Nella società medioevale il gioco d’azzardo era molto diffuso ma regolamentato. Era vietato nelle abitazioni private mentre era libero in luoghi pubblici come piazze e strade. I controlli delle autorità erano severi perché spesso, giocando d’azzardo, si perdevano beni e grosse somme di denaro e i giocatori litigavano e bestemmiavano (e questo non era tollerato dalla Chiesa).
Il “gioco pubblico”, ovvero il gioco d’azzardo che le istituzioni civili accettavano, si teneva nelle baratterie. All’inizio, erano luoghi amministrati dai Comuni che ottenevano un profitto; in seguito, le baratterie furono gestite dai privati, i barattieri, responsabili di ciò che vi succedeva e che pagavano all’erario ogni anno una somma stabilita dal comune.
Molto praticati, tra i giochi d’azzardo, erano quelli con i dadi che potevano essere sia gli aliossi (o astragali, dadi con quattro facce ricavati da ossicini di animali) sia soprattutto quelli classici (cubici, con sei facce). Tra i giochi con i dadi molto popolare nel Medioevo era il gioco della “zara” il cui nome deriva dalla parola araba “zhar” (dado) e dalla quale sembra derivare il termine “azzardo”. Anche Dante Alighieri conosceva la zara e menziona questo gioco nella Divina Commedia, all’inizio del VI canto del Purgatorio quando, insieme a Virgilio, è accerchiato dalle anime vittime di una morte violenta. Queste si affollano supplicanti poiché, riconoscendolo come vivo, gli chiedono con insistenza preghiere in loro suffragio: “Quando si parte il gioco de la zara, / colui che perde si riman dolente, / ripetendo le volte, e tristo impara; / con l’altro se ne va tutta la gente; / qual va dinanzi, e qual di dietro il prende, / e qual dallato li si reca a mente; / el non s’arresta, e questo e quello intende; / a cui porge la man, più non fa pressa; /e così da la calca si difende. / Tal era io in quella turba spessa, / volgendo a loro, e qua e là, la faccia, / e promettendo mi sciogliea da essa”.
Il sommo poeta non si paragona a chi ha perso alla zara, che triste e solo continua a lanciare i dadi e riflette sulla frequenza delle uscite dei numeri, ma al vincitore che si allontana circondato dalla folla e, proprio come quest’ultimo che promette di far festa con tutti, riesce a sottrarsi alla schiera di anime promettendo di ricordarle nelle sue preghiere.
Da luogo a luogo esistevano diverse versioni del gioco della zara; in Italia consisteva nel lanciare tre dadi dichiarando a voce alta, prima del tiro, quale sarebbe stato il risultato della somma dei punti dei tre dadi. Il vincitore era chi otteneva il risultato dichiarato. I giocatori sapevano che i possibili risultati andavano dalla somma minima di 3 a quella massima di 18 e, per esperienza, capivano che i risultati estremi 3=1+1+1 e 18=6+6+6 uscivano saltuariamente e che conveniva scommettere su 10 e 11.
Tuttavia non avevano alcuna idea del calcolo delle probabilità, la cui teoria arriverà molto più tardi.
I possibili esiti (numero delle terne di numeri da 1 a 6) nel tirare tre dadi sono 216. Infatti, lanciando un dado i casi possibili sono 6; lanciando il secondo, a ognuna delle sei possibilità del primo dado si accoppia ciascuna delle sei possibilità del secondo dado e i casi possibili diventano 6·6=36. Se, come in questo caso, i dadi sono tre abbiamo 6·6·6=216 possibili risultati. Una conclusione tutt’altro che scontata nel Medioevo quando i giocatori in realtà contavano solo 56 risultati possibili.
Per i giocatori di quel tempo, le somme 3 e 18 si potevano ottenere in un solo modo (e questo è vero), così come anche 4 e 17 (e questo non è affatto vero). Per loro dunque gli esiti 3, 4, 17, 18 erano i meno probabili. Vediamo di capire perché, considerando per esempio le somme 4 e 17. All’epoca, i giocatori non percepivano diverso l’esito (1,1,2) da (1,2,1) e da (2,1,1) e per ottenere il 4 consideravano un’unica terna, quella con due 1 e un 2. Discorso analogo per il 17: non percepivano la differenza tra (5,6,6) e (6,5,6) o (6,6,5) ma consideravano un’unica terna per ottenere il 17, quella con due 6 e un 5. In realtà 4 e 17 si possono ottenere come 4=1+1+2=1+2+1=2+1+1 e 17=5+6+6=6+5+6=6+6+5. Quindi, 4 e 17 sono tre volte più probabili di 3 e 18!
Nella pratica del gioco 3, 4, 17 e 18 erano considerati nulli (a causa dei bassi valori di probabilità, come oggi diremmo) e dunque i numeri da chiamare erano da 5 a 16. Nella successiva tabella abbiamo riportato nella prima colonna tutti i possibili esiti del lancio di tre dadi; nella seconda le terne “percepite” dai giocatori del tempo mentre nella terza colonna abbiamo inserito tutti i possibili esiti favorevoli all’uscita di una data somma. Infine, nell’ultima colonna, compaiono i valori delle probabilità (rapporti tra il numero dei casi favorevoli e quello dei casi possibili).
I giocatori ritenevano che 9, 10, 11, 12 fossero i valori più probabili, ciascuno con 6 esiti favorevoli.

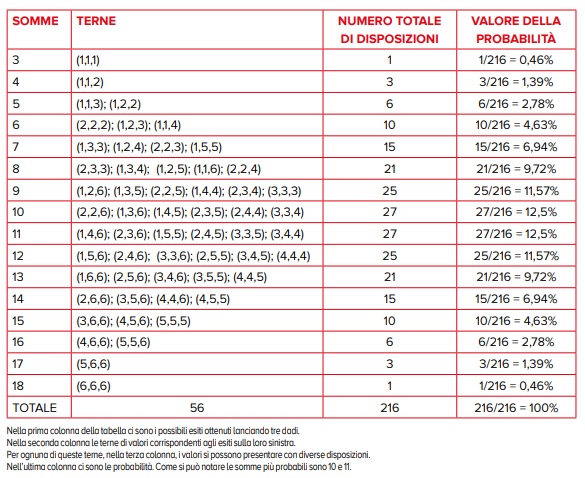
Eppure, in base alla loro esperienza pratica (insomma gioca oggi, gioca domani,…), avevano osservato che era più frequente ottenere 10 e 11 che non 9 e 12 e non riuscivano a comprendere il motivo, dato che ciascuno di questi quattro numeri poteva uscire in 6 modi. L’errore, ancora una volta, stava nel non considerare tutti i possibili esiti favorevoli che sono 27 per 10 e 11 e 25 per 9 e 12. La probabilità di ottenere 9 e 12 non è dunque 6/56 ma 25/216, cioè circa l’11,57%, mentre quella di ottenere 10 e 11 non è 6/56 ma 27/216, cioè circa il 12,5% (valore maggiore di tutti gli altri).
Il dilemma fu risolto da Gerolamo Cardano nel 1564 nel Liber de ludo aleae (pubblicato solo nel 1663) e ripreso da Galileo Galilei nel suo breve saggio Sopra le scoperte dei dadi. Questo testo fu scritto tra il 1613 e il 1623, proprio come risposta al quesito posto dal granduca di Toscana che non comprendeva come mai nella zara fosse più facile ottenere 10 e 11 rispetto a 9 e 12. Galilei risponde “che alcuni punti nel gioco dei dadi sieno più vantaggiosi di altri, vi ha la sua ragione assai manifesta, la quale è il poter quelli più facilmente e più frequentemente scoprirsi che questi, il che dipende dal potersi formare con più sorte di numeri, onde il 3 e il 18, come punti che in un sol modo si possono con tre punti comporre.” Notò, infatti, che di 216 possibili terne 27 hanno come somma 10 e 11 e solo 25 hanno come somma 9 e 12.
Per la nascita della moderna teoria della probabilità bisognerà aspettare il 1654 (quando gli studi compiuti da Cardano un secolo prima erano caduti nell’oblio) grazie alla corrispondenza scambiata tra Blaise Pascal e Pierre de Fermat, stimolati dalla domande poste dal cavaliere De Méré (Antoine Gombaud, scrittore francese e amico di Pascal), un accanito giocatore d’azzardo, su quesiti relativi al lancio dei… dadi!