La realtà ha la matematica nel sangue

I capillari sono i più piccoli vasi sanguigni del sistema circolatorio. Si stima che nel corpo umano ve ne siano circa 5 miliardi. Sono raggruppati in piccole reti dette letti capillari costituite da un numero variabile di elementi, indicativamente fra 10 e 100 a seconda dell’organo e del tipo di tessuto in cui si trovano. Ogni letto capillare è alimentato da una piccola arteria (detta arteriola terminale) e confluisce in una piccola vena (detta venula). I capillari svolgono un ruolo fondamentale nella fase di nutrizione dell’organismo perché attraverso le loro pareti si realizzano gli scambi di ossigeno e nutrienti (dal sangue ai tessuti), di anidride carbonica e di prodotti del catabolismo (dai tessuti al sangue).

Nei capillari il sangue non deve fluire troppo velocemente (altrimenti non riuscirebbero a realizzarsi le reazioni chimiche necessarie per gli scambi) né troppo lentamente (altrimenti si potrebbero generare aggregati di globuli rossi che ostruirebbero i pori dei capillari a tal punto da impedire la filtrazione delle sostanze nutritive nei tessuti). Ci chiediamo allora: da cosa è regolato il flusso del sangue nei capillari? Siamo in grado di descrivere a quale velocità scorre il sangue in un letto capillare con un modello matematico (ovvero con delle equazioni)?

Per rispondere a queste domande dobbiamo prima di tutto capire meglio il problema: che tipo di fluido è il sangue? Che conformazione hanno i capillari? Da che cosa è regolato il moto del sangue all’interno dei capillari?

Il sangue è un fluido piuttosto complesso che presenta una componente corpuscolare (globuli rossi, globuli bianchi e piastrine) e una liquida (il plasma). La concentrazione della parte corpuscolare nel plasma non è sempre la stessa, ma varia in funzione delle caratteristiche geometriche del vaso sanguigno in cui il sangue sta scorrendo e ne influenza la velocità. Inoltre il sangue è un fluido con una viscosità non costante. Ciò significa che, se all’interno di un vaso sanguigno di forma cilindrica potessimo sezionare il sangue in tanti cilindri concentrici, l’attrito che si genererebbe durante il moto tra due cilindri adiacenti potrebbe essere diverso da quello che si creerebbe tra altri due cilindri adiacenti. I capillari hanno una forma molto contorta, sono deformabili e le loro pareti sono permeabili, cioè presentano piccolissimi fori per consentire gli scambi tra sangue e tessuti. Il cuore è il motore di tutto l’apparato cardio-circolatorio: ad ogni battito, il ventricolo sinistro pompa il sangue ossigenato nell’aorta e la forza esercitata induce sulle pareti di tutti i vasi sanguigni una pressione, detta pressione sanguigna. Nell’arco di un battito la pressione varia da un valore massimo (la pressione sistolica) a un valore minimo (la pressione diastolica) e, a mano a mano che il sangue fluisce dall’aorta ai capillari e da lì ritorna all’atrio destro del cuore, la pressione media (pari alla somma di un terzo della pressione sistolica e di due terzi di quella diastolica) diminuisce. Sono proprio i diversi valori di pressione nei diversi punti del sistema circolatorio a indurre il moto del sangue nei vasi sanguigni. Più precisamente, all’interno di un qualsiasi vaso sanguigno, il sangue si muove da regioni a pressione maggiore verso regioni a pressione minore. Formulare un modello matematico che descriva il moto del sangue nei capillari tenendo conto di tutti questi aspetti è veramente molto complicato, se non addirittura impossibile, ma ne vale la pena. Bisogna, però, introdurre delle semplificazioni. Nonostante ci allontanino dalla realtà nella sua completezza, esse ci consentono infatti di fornire una rappresentazione accettabile del fenomeno che vogliamo analizzare. Assumiamo allora che la viscosità del sangue nei capillari sia costante e che le pareti dei capillari siano rigide e non elastiche (in effetti, l’elasticità è molto più pronunciata nelle grandi arterie che nei capillari). Supponiamo poi che ogni capillare sia assimilabile a un tubo cilindrico, trascuriamo i processi chimici di scambio dei liquidi con i tessuti circostanti e, infine, consideriamo semplici letti capillari. A questo punto, per poter derivare un modello matematico che permetta di calcolare la velocità del sangue in ogni capillare di un letto, dobbiamo capire che cosa succede in un singolo capillare e, anzitutto, dobbiamo far riferimento ad alcuni principi di fluidodinamica (quella parte della fisica che studia il moto dei fluidi). In particolare ci servono: il concetto di portata di un condotto (la portata è la quantità di fluido che attraversa la sezione di un condotto nell’unità di tempo); la legge di Poiseuille, con cui possiamo calcolare la portata a partire dalle caratteristiche geometriche del condotto (la lunghezza L e il raggio r), dalla viscosità μ del fluido e dai valori p₁ e p₂ di pressione agli estremi del condotto e infine una relazione di proporzionalità tra la portata e la velocità media v con cui il fluido scorre nel condotto. Mettendo insieme questi ingredienti otteniamo:

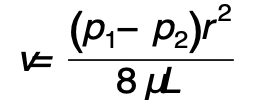
Questo è il modello matematico che adottiamo per calcolare la velocità media del sangue in un singolo capillare, a patto che siano noti tutti i dati che compaiono nel termine destro dell’equazione. Abbiamo costruito un modello: se abbiamo i dati, possiamo calcolare la soluzione. Ora che sappiamo come calcolare la velocità del sangue in un singolo capillare, consideriamo un semplice letto capillare come quello mostrato nell’immagine a sinistra e rappresentiamolo con un grafo (immagine di destra). Un grafo è un’astrazione matematica costituita da nodi (i cerchietti bianchi) e archi (le linee nere). Qui ogni arco rappresenta un capillare, mentre i nodi sono i punti in cui confluiscono due o più vasi (capillari, arteriola, venula).

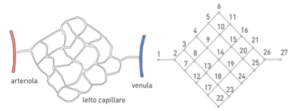
Supponendo che i capillari siano sempre condotti cilindrici di cui conosciamo lunghezza e raggio e che il sangue abbia viscosità costante, potremmo applicare ad ogni capillare il modello che abbiamo descritto prima. Ci rendiamo però immediatamente conto che, per determinare la velocità media in ogni capillare, dovremmo conoscere i valori di pressione agli estremi di ogni capillare, cioè in tutti i nodi del letto. In realtà, ciò di cui disponiamo sono solo il valore della pressione sanguigna nei punti a contatto con l’arteriola e la venula (cioè nei nodi 1 e 27 del grafo)! Come possiamo calcolare le pressioni in tutti gli altri nodi? L’aiuto ci è dato dalle equazioni di bilancio. Visto che abbiamo supposto che le pareti dei capillari siano impermeabili, il sangue non si può formare dal nulla e allo stesso tempo non può sparire nel nulla, ma la quantità totale di sangue che arriva in un nodo deve eguagliare la quantità totale di sangue che esce dal nodo stesso (pensate a un incrocio stradale: le auto che arrivano all’incrocio devono anche uscire dall’incrocio). Questa è un’equazione di bilancio e abbiamo tante equazioni di bilancio quanti sono i nodi del grafo. Otteniamo quindi un sistema di equazioni lineari, detto sistema delle equazioni di bilancio, le cui incognite sono i valori della pressione sanguigna nei nodi del grafo. Questo è il modello matematico che ci permette di calcolare i valori di pressione in tutti i nodi del grafo. Nell’esempio del grafo riportato in figura, i nodi (e quindi le incognite) sono 27. Una volta che abbiamo trovato i valori di pressione nei nodi del grafo, possiamo applicare il modello matematico relativo a un singolo capillare e trovare la velocità media del sangue in ogni capillare. Possiamo essere soddisfatti del nostro lavoro? Non completamente: le formule che ci permettono di determinare la velocità media del sangue nei capillari presentano un’evidente difficoltà. Calcolare a mano la soluzione di un sistema lineare di 27 equazioni e 27 incognite (tante quanti sono i nodi del nostro letto capillare) non è banale… Entrano allora in gioco la modellistica numerica e il calcolo scientifico che ci permettono di formulare metodi numerici e algoritmi efficienti da tradurre in codici eseguibili su un computer, in modo da ottenere una soluzione (cosiddetta computazionale) che è un’approssimazione della soluzione del modello matematico.

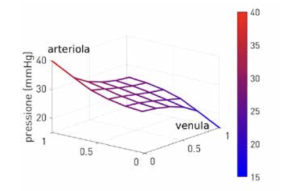
Poi, però, dobbiamo verificare che la soluzione computazionale sia in accordo con i dati sperimentali. È possibile, allora verificare che i valori della pressione sanguigna trovati con il modello matematico diminuiscono all’interno del letto capillare a mano a mano che il sangue procede dall’arteriola alla venula, in accordo con quanto accade nella realtà. Invece, la velocità media del sangue nei capillari assume valori compresi tra 0.06 e 0.66 mm/s (che sono valori realistici) e risulta maggiore nei capillari più vicini all’arteriola e alla venula e minore nei capillari più centrali.

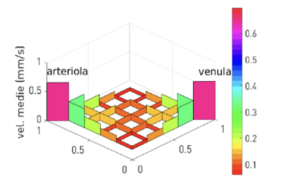
E se ora volessimo costruire un modello più realistico? Ad esempio potremmo studiare che cosa succede quando un atleta sta producendo uno sforzo fisico o quando un individuo è soggetto ad anemia o, ancora, quando assume un farmaco. In questi casi, dovremmo eliminare via via le semplificazioni che abbiamo introdotto all’inizio e proporre nuove equazioni sempre più complesse. Il payoff sarà la possibilità di fornire al medico risposte più significative (qualitativamente e quantitativamente) a supporto della diagnosi e della cura.