Giochi matematici – Ma non c’è una soluzione più semplice?

Capita che alcuni nostri lettori talvolta “si arrabbino” quando leggono le soluzioni che i giochisti di Prisma propongono nel dossier dedicato ai giochi matematici. “Si arrabbiano” soprattutto quando trovano la soluzione da noi data troppo pesante e macchinosa, con strumenti da scuole superiori senza che ve ne sia una reale necessità… o almeno questo è quello che ci dicono. Naturalmente a noi il dibattito fa solo piacere e li invitiamo a fornirci le loro soluzioni. In questa rubrica ve le proponiamo, deciderete poi voi lettori quali siano le migliori! Questa volta la soluzione è stata trovata dagli alunni di Sofia Sabatti, che ci ha scritto. Non si sono “arrabbiati”, anzi, nelle loro parole troviamo la gioia della scoperta di una via inaspettata di soluzione.

Gioco 9 delle semifinali dei Campionati Internazionali di Giochi Matematici, soluzione pubblicata su Prisma 30 (maggio 2021)

9 INSCRITTO O CIRCOSCRITTO

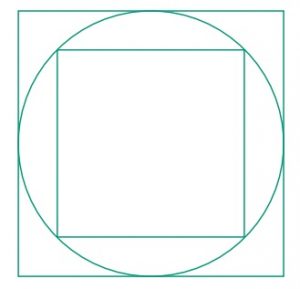
In figura vedete un quadrato inscritto in una circonferenza e un altro quadrato, circoscritto alla stessa. Esprimete con una frazione irriducibile il rapporto tra l’area del quadrato piccolo e quella del quadrato grande.

Soluzione di Prisma

9 INSCRITTO O CIRCOSCRITTO

Se r è il raggio della circonferenza, abbiamo subito che il lato del quadrato più grande è L=2r. Detto l il lato del quadrato più piccolo, dal teorema di Pitagora ricaviamo l²=2r². Ne segue che il rapporto fra le aree richiesto è: l²/L²=2r²/4r²=1/2.

Soluzione alternativa proposta

Ho proposto INSCRITTO O CIRCOSCRITTO ai 23 alunni di una mia prima media e l’hanno risolto in due, entrambi senza ricorrere al teorema di Pitagora. Quando ho chiesto loro di spiegare ai compagni come avevano fatto, dopo aver confabulato qualche istante, mi hanno detto che avrebbero avuto bisogno di un marchingegno. Pensavo che stessero scherzando e ho chiesto loro, ridendo, se si trattava di una cosa che potevano costruire; seri come non mai, mi han detto che avevano solo bisogno di un fermacampioni e quindi mi sono data da fare per procurarlo. Il giorno dopo sono arrivati a scuola con l’affare che potete vedere in foto.

Hanno ritagliato due quadrati di cartoncino, uguali se non per il colore. Su uno dei due hanno incollato un cerchio, inscritto nel quadrato stesso. All’altro quadrato hanno fatto quattro pieghe, per portare i quattro vertici nell’incontro delle diagonali, ottenendo così un quadrato inscrivibile nel cerchio inscritto al primo. Hanno poi incernierato i due quadrati con il fermacampioni nel loro centro. Hanno iniziato a mostrare il marchingegno ai compagni, tenendo il secondo quadrato (quello “inscritto”) con i lati paralleli ai lati del quadrato circoscritto (come nella figura del gioco); hanno poi iniziato a farlo ruotare piano piano, come prestigiatori che cerchino di tenere il pubblico in sospeso. In realtà c’è stato un coro scomposto di “Ma sì! Adesso abbiamo capito!” ancora prima che il quadrato piegato completasse il quarto di giro e ancor prima che i due prestigiatori ne aprissero i quattro lembi per raddoppiarne l’area e farlo sovrapporre al quadrato circoscritto.
Ho fatto loro i complimenti e mi sono impadronita del marchingegno. Quando sono arrivata in terza, ce l’avevo ancora in mano e ovviamente i miei alunni, sempre pronti a tentare di perdere tempo, hanno iniziato a chiedermi di che si trattasse. L’ho appoggiato alla lavagna nella posizione che richiama il disegno del gioco. Non ho fatto in tempo a proferire parola che uno di loro, che aveva partecipato alle semifinali e non era riuscito a rispondere a questo quesito, se ne è uscito (ovviamente ad alta voce) con un bel “Che stupido!”. “Stupido chi?”, gli ho chiesto io, già quasi furibonda. “Stupido io che non me ne sono accorto. Avevo cercato di applicare Pitagora usando le lettere al posto dei numeri, ma mi ero incastrato senza riuscire a venircene fuori. Così invece si vede subito, senza lettere e senza radici quadrate”.

Ha ragione, no?