I block-notes: I modelli matematici

CHE COS’E’ UN MODELLO MATEMATICO

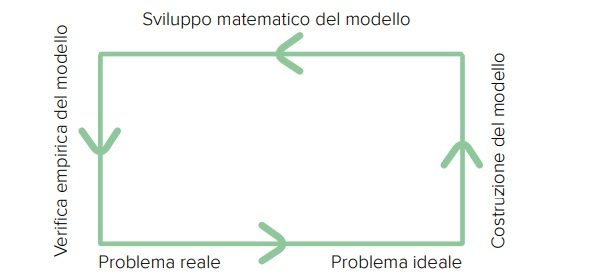
È come un ascensore che collega la realtà alla matematica, andata e ritorno. Ecco le fasi del suo viaggio.

1

Il punto di partenza è rappresentato da un problema reale, concreto, di cui non si riesce a venire a capo usando semplicemente il buon senso e gli ordinari ragionamenti. Per esempio: la previsione della diffusione di una pandemia. Si decide allora di ricorrere alla matematica, che non serve dunque per fare esercizi o risolvere rompicapo astrusi ma per affrontare questioni complesse.

2

Il problema difficile rimane tale anche per il matematico che infatti, per mettersi al lavoro, decide preliminarmente di semplificarlo. Trascura gli elementi che gli sembrano secondari e fissa la sua attenzione su quelli essenziali. Considera insomma un problema ideale. Questa semplificazione è una costruzione soggettiva: dipende dal problema in questione ma anche dalla tradizione matematica, dalla sensibilità del ricercatore, dal suo “naso”. Nell’esempio della pandemia, possiamo pensare che il nostro ricercatore abbia scelto come elementi essenziali il tempo e la numerosità di alcune “popolazioni”, in particolare i suscettibili di infezione, gli infetti e gli isolati (se segue il classico modello di Kermack e McKendrick del 1927).

3

Comincia l’effettiva costruzione del modello. Tra gli elementi essenziali ce ne sono alcuni che sembrano influenzare gli altri: se cambiano, anche gli altri cambiano e secondo una certa legge. Nascono in altre parole le variabili indipendenti – il tempo, nel caso della pandemia – e quelle dipendenti, che sono funzione delle prime e che nel nostro esempio variano dunque al variare del tempo. La questione iniziale – come si evolverà la pandemia – consiste ora nel capire la forma delle funzioni che esprimono il numero dei suscettibili, degli infetti ecc. in funzione del tempo. Queste funzioni, la loro forma e i valori assunti, sono le nostre incognite. La pandemia si sarà estinta quando il numero dei nuovi infetti sarà nullo; si potrà ritenere di aver superato la fase più critica quando il numero dei ricoverati in terapia intensiva rimarrà al di sotto di una certa soglia. Il problema iniziale è stato insomma tradotto in un sistema di misurazioni, che permette a tutti noi di valutare lo stato in cui il sistema si trova. Non dobbiamo comunque dimenticare le approssimazioni che si è convenuto di introdurre per operare questa traduzione nel linguaggio matematico e che ugualmente permettono di scrivere le relazioni tra le incognite, ossia le equazioni che costituiscono il modello e dalla cui soluzione verrà la risposta al problema iniziale. Sono spesso equazioni differenziali, basate sulle velocità con cui le funzioni incognite variano. Ad esempio: sembra realistico pensare che la velocità con cui cresce il numero dei malati isolati sia proporzionale al numero degli infetti.

4

Con la costruzione del modello, quello che abbiamo ritenuto più adeguato, abbiamo tradotto il problema iniziale in formule. L’ascensore ha terminato la salita e ci troviamo ora sul piano più propriamente matematico. La manipolazione dei simboli ci può rivelare conclusioni a cui gli ordinari ragionamenti non riuscivano ad arrivare  o far capire come gli scenari possono cambiare al variare di determinate situazioni. Naturalmente, per risolvere l’equazione o il sistema di equazioni che abbiamo costruito occorre conoscere il calcolo, algebrico o differenziale che sia. Nella realtà, ci pensa il computer a macinare le tante equazioni in tante incognite che costituiscono il modello e a fornirci la soluzione.

5

L’accuratezza previsionale del modello dipende da alcuni dati che abbiamo inserito. Sono le cosiddette condizioni iniziali. La soluzione trovata è giusta, anche perché i calcoli… li ha fatti il computer, ma il momento della verifica empirica è essenziale per testare la significatività del modello: può darsi che la risposta fornita, pur giusta, si riveli in contrasto con altre nostre informazioni o, nell’esempio che ci ha accompagnato, inadeguata a fotografare lo sviluppo della pandemia e a prevederne l’evoluzione con sufficiente esattezza. Bisogna allora inserire dei dati più accurati oppure pensare che le semplificazioni introdotte nella costruzione del modello siano state eccessive oppure, ancora, cambiare radicalmente approccio. Con l’umiltà di chi sa riconoscere la parzialità del proprio lavoro ma anche sapendo che in molti casi – si pensi di nuovo al coronavirus – alternative ai modelli matematici e al metodo scientifico non ce ne sono. A meno che non si voglia ricorrere ai tarocchi, all’astrologia o alle profezie di Nostradamus.