I block-notes: La distanza

VA ALLA GRANDE

Non si parla altro che di distanziamento sociale. Tutti corrono a misurare la distanza tra un ombrellone
e l’altro e i metri che devono separare due tavoli in un ristorante. Per il concetto di distanza non c’è stato forse periodo migliore, complice anche il fatto che tra tanti virus, virologi, epidemiologi, matematici della gaussiana emerge finalmente un’idea semplice, alla portata di tutti. Le distanze: capiamo di che cosa si tratta e le sappiamo calcolare!

ELEMENTARE WATSON

Effettivamente l’idea di distanza tra due punti P1 e P2 di un piano non sembra nascondere segreti: la distanza è il
segmento che li congiunge o, meglio, la sua lunghezza. Finalmente una nozione matematica molto concreta e legata alla realtà! Chi ha più freschi gli insegnamenti scolastici, in particolare di geometria analitica, ricorda addirittura la formula che permette di calcolarla. Nel terzo anno delle superiori, o anche prima, la sapeva ricavare come semplice applicazione del teorema di Pitagora:

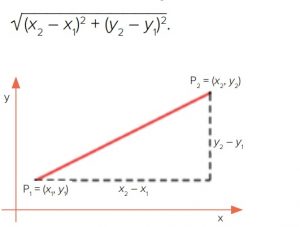
…NON PROPRIO

La formula della radice quadrata non si può però applicare se dobbiamo calcolare la distanza tra due punti di una città a pianta ortogonale, dove le strade si intersecano ad angolo retto. Qui, la distanza tra i due punti P1= (x1, y1) e P2= (x2, y2) è data dalla lunghezza del tratto orizzontale sommata con quella del tratto verticale: (x2-x1) + (y2-y1). Quella della radice quadrata era la distanza in linea d’aria. La nuova distanza viene chiamata distanza della torre perché descrive bene come si muove la torre nel gioco degli scacchi, solo in orizzontale e in verticale.

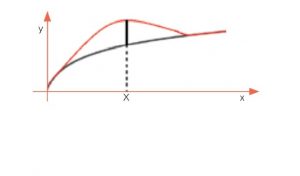
Ma c’è di più. In tempi di coronavirus i matematici fanno le previsioni sull’andamento del contagio. Supponiamo che la curva rossa rappresenti l’andamento effettivo del contagio e quella nera l’andamento nelle previsioni del modello. Erano previsioni azzeccate o no? In altre parole, qual è risultata la distanza tra il fenomeno reale e l’andamento previsto? Altro che elementare: qui si tratta di calcolare la distanza tra due curve. Come fare?

CI PENSA FRÉCHET

La consapevolezza che non c’è un’unica formula per misurare la distanza tra due punti del piano o dello spazio, e quindi che non c’è un’unica idea di distanza, si è consolidata tra i matematici nella seconda metà dell’Ottocento.
Risultava sempre più opportuno uscire dalla logica dell’elenco di formule, una per ogni caso specifico, e tentare invece di dare una definizione di carattere generale che catturasse in qualche modo gli aspetti irrinunciabili del concetto di distanza. L’ha fatto il matematico francese Maurice Fréchet (1878-1973) che, nella sua tesi di dottorato
del 1906, ha introdotto gli spazi metrici, dando quella che è considerata la definizione moderna di distanza.
La tesi di Fréchet è stata pubblicata su una rivista scientifica italiana, i Rendiconti del Circolo matematico di Palermo.

TRE CONDIZIONI

La distanza d tra due punti X e Y è un qualsiasi numero, che associamo a X e a Y. I matematici scrivono d(X,Y) per indicare che d dipende dalla posizione di X e Y. Non proprio un qualsiasi numero, in realtà. Anzitutto d(X,Y) deve essere positivo (non ha senso una distanza negativa) e uguale a 0 se e solo se X e Y coincidono. La distanza d, inoltre, è un qualsiasi numero positivo (nullo quando X=Y) che però deve soddisfare la condizione d(X,Y)=d(Y,X) in quanto la distanza rimane inalterata se cambiamo il verso di percorrenza. Infine, se per andare da X a Y si fa una deviazione per un terzo punto Z, la distanza aumenta; ecco allora la terza proprietà da soddisfare d(X,Y) ≤ d(X,Z) + d(Z,Y).
Morale: di distanza non ce n’è una sola e ognuno è libero di scegliere quella che vuole, purché la sua formula soddisfi le tre condizioni che abbiamo descritto e che sono irrinunciabili in qualunque espressione matematica che ambisca a chiamarsi distanza.

LA MATEMATICA E’ SOGGETTIVA?

Torniamo all’esempio delle due curve, quella dell’andamento effettivo del contagio e quella delle previsioni. Chi vorrà sottolineare l’inattendibilità del modello matematico, da cui le previsioni sono scaturite, prenderà come distanza tra le due curve il massimo scarto, quello più eclatante, che si è registrato il giorno X (vedi la figura delle curve rossa e nera). Chi invece vuole sottolineare come nel complesso le previsioni siano risultate accurate sceglierà come distanza tra le due curve un numero riferito al loro andamento in tutto il periodo considerato, ad esempio un
numero legato all’area della superficie compresa tra i due grafici. Ciascuno è libero di fare come meglio crede, purché
la distanza scelta soddisfi le tre proprietà che abbiamo descritto prima. In questo modo di procedere non c’è niente
di cui scandalizzarsi. La matematica è composta da numeri e simboli che traducono le idee e queste possono essere diverse. La matematica non aggiunge una certezza che non c’è; traduce le nostre idee in un linguaggio libero da molte delle imprecisioni e degli equivoci che contraddistinguono il linguaggio comune. Soprattutto, quello matematico è un linguaggio che si presta a essere trasformato con i calcoli, con successive elaborazioni che possono arrivare a conclusioni a cui il linguaggio naturale non riusciva a pervenire.