I giochi matematici della settimana

Una famiglia

In problemi di questo tipo, che sono apparentemente dei rompicapo,il linguaggio delle equazioni aiuta non poco. Sia m il numero dei maschi e f quello delle femmine. L’informazione che ogni ragazza ha tanti fratelli quante sorelle porta a dire che il numero delle ragazze è superiore di uno a quello dei ragazzi: f = m + 1. Allo stesso modo,
dall’informazione che ciascun ragazzo ha un numero di sorelle f che è tre volte quello dei suoi fratelli m − 1, ricaviamo l’uguaglianza f = 3 (m − 1). Bisogna allora cercare le soluzioni intere del sistema:
f = m + 1
f = 3 (m − 1)
Otteniamo così f = 3 e m = 2, da cui f + m = 5.

Alle prese con l’ottagono

Ogni volta che si traccia un segmento che unisce due punti del contorno di una figura, si crea una nuova regione:

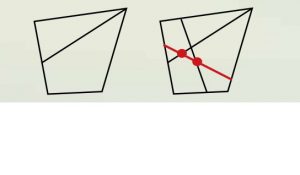
Anche per ogni intersezione con altri segmenti già esistenti si crea una nuova regione. Si tratta quindi di contare segmenti (nel nostro caso le diagonali dell’ottagono) e intersezioni. Il numero delle diagonali è dato dal numero delle combinazioni di 8 oggetti, presi a due a due, al quale bisogna però sottrarre il numero dei lati. Le diagonali dell’ottagono risultano allora 20. Per contare le intersezioni delle diagonali (esclusi i vertici) numeriamo gli stessi
vertici da 1 a 8. A ogni quaterna di interi (per esempio la quaterna {2, 3, 5, 8}) possiamo associare un’unica intersezione (nell’esempio che stiamo facendo, l’intersezione tra la diagonale 2-5 e la diagonale 3-8). Il numero delle quaterne è dato dal numero delle combinazioni di 8 oggetti presi a 4 a 4. Risultano 70. La somma del numero di diagonali e intersezioni è allora uguale a 90. Ma non dobbiamo dimenticare che all’inizio avevamo già una regione.
L’ottagono è quindi diviso al massimo in 20 + 70 + 1 = 91 regioni.

I numeri di Nando

Provando a elencare i numeri richiesti, si notano alcune regolarità. Da 10.059 a 10.095 sono 5. Da 10.149 a 10.194 sono 6. Poi sono 7, 8, 9, 10, 9, 8, 7, 6 fino a 10.905: in totale 75. Da 11.049 a 11.094 sono 6. Da 11.139 a 11.193 sono 7. Poi sono 8, 9, 10, 9, 8, 7, 6, 5 fino a 11.904: in totale 75. Ne abbiamo poi 73, 69, 63, 55, 45, 36, 28, 21 fino a 19.500. In totale, abbiamo 540 numeri che iniziano con 1. Proseguendo con i numeri che iniziano con 2, si vede che sono 75 +
73 + 69 + 63 + 55 + 45 + 36 + 28 + 21 + 15 = 540 – 75 + 15 = 480.
I numeri che iniziano con 3 sono: 73 + 69 + 63 + 55 + 45 + 36 + 28 + 21 + 15 + 10 = 480 – 75 + 10 = 415.
I numeri che iniziano con 4 sono: 69 + 63 + 55 + 45 + 36 + 28 + 21 + 15 + 10 + 6 = 415 – 73 + 6 = 348.
Siamo già arrivati a 540 + 480 + 415 + 348 = 1.783 numeri, ci siamo quasi…
I numeri che iniziano con 5 saranno 63 + 55 + 45 + 36 + 28 + … ma con il 54.600 siamo già a 2.010 numeri. Ne mancano solo otto: 55.005, 55.014, 55.023, 55.032, 55.041, 55.050, 55.104, 55.113.
Il 2.018esimo numero è 55.113.