Giochi matematici – Ma non c’è una soluzione più semplice???

Capita che alcuni nostri lettori talvolta “si arrabbino” quando leggono le soluzioni che i giochisti di Prisma propongono nel dossier dedicato ai giochi matematici. “Si arrabbiano” soprattutto quando trovano la soluzione da noi data troppo pesante e macchinosa, con strumenti da scuole superiori senza che ve ne sia una reale necessità… o almeno questo è quello che ci dicono. Naturalmente a noi il dibattito fa solo piacere e li invitiamo a fornirci le loro soluzioni. In questa rubrica ve le proponiamo, deciderete poi voi lettori quali siano le migliori! Questo è il turno di Maria Dedò!

Gioco 13 (comparso su Prisma 20 di giugno 2020)

UN RAPPORTO, QUESTA VOLTA, TRA DUE LUNGHEZZE

I triangoli ABC e ADE, entrambi rettangoli in A, hanno i lati a due a due uguali. L’area del quadrilatero ADFB è uguale alla somma delle aree dei triangoli CFD e BFE. Qual è allora il rapporto tra la misura di AB e quella di AC?

Soluzione di Prisma

Conviene orientare diversamente la figura, così che si potrebbe procedere anche con un sistema di riferimento cartesiano e la geometria analitica.

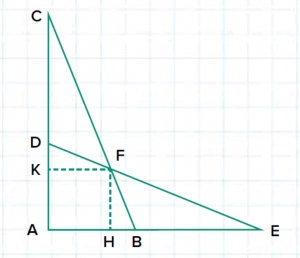
Procediamo invece per via geometrica e poniamo AH=AK=HF=KF=x, HE=KC=y. I triangoli HEF e KFD sono simili; allora DK:x=x:y; DK=x2/y e BE=y–(x2/y)=(y2–x2)/y. Calcoliamo le aree delle varie figure: Area(AHFK)=x2, Area(HEF)=xy/2, Area(HBF)=x3 /2y, Area(ABFD)=x2(y+x)/y, Area(BEF)=x(y2–x2)/2y. Area(BEF)+Area(CDF)= 2Area(BEF)= x(y2–x2)/y. Uguagliando queste ultime due aree e semplificando, risulta x=y–x da cui y=2x. Allora: AE=x+y=x+2x=3x e AB=AH+HB=x+x2/y=(xy+x2)/y=3×2/2x=(3/2)x. Otteniamo infine AB/AE=(3/2)x/3x=1/2.

Soluzione alternativa proposta

Una soluzione (più semplice) che non usa la geometria analitica è la seguente. La retta per A e F è asse di simmetria della figura. Quindi sono uguali fra loro i triangoli FBE e FDC e anche i triangoli AFB e AFD. La condizione che dà il testo sull’area del quadrilatero garantisce che sono uguali anche le aree dei due triangoli AFB e FBE, cioè FB è la mediana del triangolo AFE, sicché: AB/AC=AB/AE=1/2.

Inoltre:

• (nel testo) l’angolo in A è segnato come retto, ma in figura è visibilmente non retto.
• non è bello il commento all’inizio della soluzione: sembra quasi che non si possa usare un sistema di riferimento con una figura “non dritta”! È una cosa di poco conto, ma “asseconda” una serie di stereotipi molto diffusi (dalla scuola primaria agli adulti usciti da scuola) come per esempio il fatto che un quadrato con i lati non paralleli ai bordi del quaderno o della lavagna è un rombo e non è un quadrato.