Soluzioni dell’8 settembre 2025 a cura di Fabio Ciuffoli
Ieri abbiamo presentato 3 problemi prendendo spunto dai sitemi elettorali proporzionali e maggioritari utilizzati nelle moderne democrazie. Di seguito pubblichiamo le nostre proposte di soluzione.
Democrazia, circoscrizioni elettorali e maggioranze – soluzioni
In ciascuna delle griglie sottostanti, il problema consiste nel disegnare una mappa elettorale unica in cui il colore di minoranza vince il maggior numero di regioni. Una regione è definita come un blocco contiguo di celle unite orizzontalmente o verticalmente, una regione non può contenere celle collegate solo diagonalmente. Vincere una regione significa avere il maggior numero di celle in quella regione.
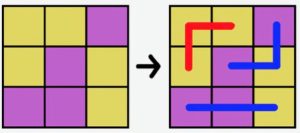
Iniziamo con un esempio semplice. Dividere la griglia in 3 regioni da 3 celle ciascuna in modo che il viola, il colore di minoranza, vinca il maggior numero di regioni? In figura a sinistra è illustrato il problema e a destra la soluzione.
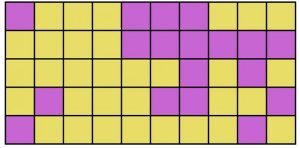
Problema 1. (Facile) Dividere la griglia in 5 regioni da 5 celle ciascuna in modo che il viola, colore di minoranza con 9 regioni su 25, vinca nel maggior numero delle regioni.

Per le versioni stampabili e per esercitarsi click qui.
1. SOLUZIONE
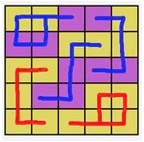
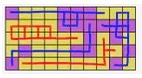
Problema 2. (Medio) Dividere la griglia in 5 regioni da 10 celle ciascuna modo che il viola, colore di minoranza, vinca nel maggior numero delle regioni. Non sono ammessi pareggi nelle regioni.
2. SOLUZIONE
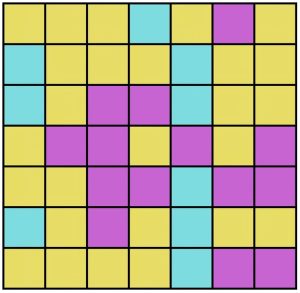
Problema 3. (Difficile) In questo caso ci sono tre contendenti. Dividere la griglia in 7 regioni da 7 celle ciascuna in modo che l’azzurro , colore di minoranza, vinca nel maggior numero di regioni. Non sono ammessi pareggi per il primo posto in alcuna regione.
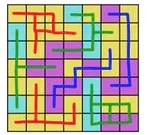
3. SOLUZIONE
I Giochi del Lunedì di Prisma tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).