I Giochi del Lunedì di Prisma dell’8 settembre 2025 a cura di Fabio Ciuffoli
I problemi che proponiamo oggi prendono spunto da un provvedimento firmato dal governatore repubblicano del Texas nello scorso mese di agosto che ridisegna i confini delle circoscrizioni elettorali con l’evidente scopo di avvantaggiare il suo partito. In risposta il governatore democratico della California sta reagendo nello stesso modo nel suo Stato. In effetti si tratta di uno stratagemma, chiamato Gerrymandering, che a prescindere dalla natura politica nasconde alcuni interessanti calcoli e stimola qualche riflessione sui sistemi elettorali proporzionali o maggioritari nelle attuali democrazie. Ad esempio: data una certa distribuzione degli elettori, come si traccia una mappa in modo che al partito di minoranza venga assegnata la maggioranza delle circoscrizioni o viceversa? È questa la domanda alla base dei tre problemi illustrati di seguito. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio dei commenti, domani alle ore 17.00 pubblicheremo le nostre proposte di soluzione.
Democrazia, circoscrizioni elettorali e maggioranze.
In ciascuna delle griglie sottostanti, il problema consiste nel disegnare una mappa elettorale unica in cui il colore di minoranza vince il maggior numero di regioni. Una regione è definita come un blocco contiguo di celle unite orizzontalmente o verticalmente, una regione non può contenere celle collegate solo diagonalmente. Vincere una regione significa avere il maggior numero di celle in quella regione.
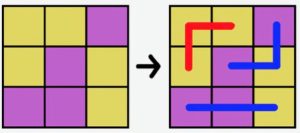
Iniziamo con un esempio semplice. Dividere la griglia in 3 regioni da 3 celle ciascuna in modo che il viola, il colore di minoranza, vinca il maggior numero di regioni? In figura a sinistra è illustrato il problema e a destra la soluzione.
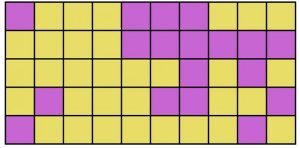
Problema 1. (Facile) Dividere la griglia in 5 regioni da 5 celle ciascuna in modo che il viola, colore di minoranza con 9 regioni su 25, vinca nel maggior numero delle regioni.

Per le versioni stampabili e per esercitarsi click qui.
Problema 2. (Medio) Dividere la griglia in 5 regioni da 10 celle ciascuna modo che il viola, colore di minoranza, vinca nel maggior numero delle regioni. Non sono ammessi pareggi nelle regioni.
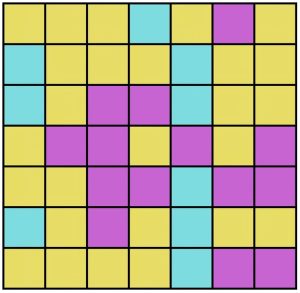
Problema 3. (Difficile) In questo caso ci sono tre contendenti. Dividere la griglia in 7 regioni da 7 celle ciascuna in modo che l’azzurro , colore di minoranza, vinca nel maggior numero di regioni. Non sono ammessi pareggi per il primo posto in alcuna regione.
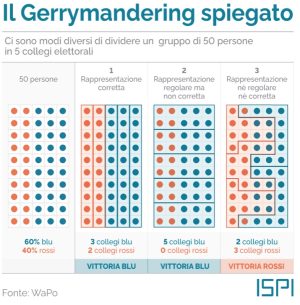
Per spiegare sinteticamente il concetto di Gerrymandering proponiamo la seguente pagina dell’ISPI (Istituto per gli Studi di Politica Internazionale). In questo esempio ci sono 50 elettori (20 rossi e 30 blu) da suddividere in 5 collegi. Nella suddivisione in colonna 1 è riportato il risultato simile al sistema proporzionale; nella colonna 2 il risultato è a favore del blu e nella 3 con qualche forzatura il risultato è a favore dei rossi.
I problemi sono stati ideati da Brady Forrest, uno studente universitario di Toronto il cui alias online è Deckard, che ringraziamo per la condivisione. Nei suoi video su YouTube parla della matematica che sta alla base di questi problemi e mostra come risolverli.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
7 risposte
Per vincere in un collegio, il rosa deve essere presente in almeno 3 caselle su 5.
Quindi, essendoci 9 caselle rosa, il massimo numero possibile di collegi in cui il rosa può vincete è 9/3 = 3.
Per raggiungere questo risultato massimale teorico devono quindi potersi disegnare 2 collegi costituiti solo da caselle gialle, e questo può essere fatto in un unico modo: dividendo in due il “serpentone” giallo in basso. Fatto questo, il resto è quasi immediato. Vedi immagine allegata.
Per il problema 3,
dall’analisi dei numeri in gioco si deduce che gli azzurri (accreditati di soli 9 seggi totali) per vincere la tornata elettorale dovranno vincere in 3 collegi (da 7 seggi), e quindi in ciascuno si dovrà avere il risultato: 3 azzurri + 2 gialli + 2 viola.
I restanti 4 collegi dovranno andare equamente agli altri due partiti, in questa forma: due da 7g e due da 4v+3g
Quesito 2a.
Stessa strategia; ottengo tre regioni in cui il viola vince per 6 a 4, e due regioni in cui il giallo vince per 10 a 0.
In totale così il partito viola vincerebbe le elezioni, pur avendo la maggioranza solo in 18 seggi su 40.
ops! 18 su 50
cioè poco più di un terzo
NB: Fabio, non sarebbe male (se possibile!) implementare una funzione di modifica dei commenti 😉
Lo farò presente ai tecnici. Grz.
Ho iniziato da quelli facili, anche l’altro presente nel file in link.
Le mie soluzioni sono allegate nell’immagine.
La strategia mi sembra quella di accorpare il più possibile i seggi maggioritari in collegi dello stesso colore (in pratica regioni con 5 celle tutte gialle) e d’altra parte unire i seggi minoritari (viola) in collegi con un minimo vantaggio sugli avversari (regioni in cui i viola vincono 3 a 2 sui gialli).
Ovviamente a livello reale, in politica (da cui nasce in effetti questa tua proposta di Giochi) questa “strategia” si basa sull’assunzione che i singoli seggi rimangano sicuri e immutabili, o quasi, rispetto alle elezioni precedenti.
Mi viene in mente che anche in Italia nel recente passato vari governi proponevano riforme elettorali nell’intimo convincimento di trarne maggior vantaggio alle future elezioni. Ma a volte …sono rimasti gabbati dai risultati effettivi, mentre la precedente legge elettorale li avrebbe premiati. 🙂
Ottime e acute osservazioni. In Italia è andata esattamente come hai detto. Siamo di fronte a professionisti della politica o improvvisatori? Quello che mi preoccupa è la nostra democrazia fragile, un po’ malata e con scarsa partecipazione, che poco interessa ai nostri professionisti/improvvisatori. Ma noi andiamo avanti, anche con i giochi.