Pubblichiamo le soluzioni della quarta e ultima Tappa del Tour giochistico di PRISMA 2025.
A seguire le classifiche di tappa.
Quanti!
I numeri in questione sono della forma abbb con 0<a<b. Per capire quanti sono questi numeri, consideriamo i possibili valori assunti da a. Per a=1, b può assumere tutti i valori (interi) da 2 a 9, inclusi: abbiamo 8 possibilità. Per a=2, abbiamo 7 possibilità in quanto b può assumere tutti i valori (interi) da 3 a 9. Si continua a ragionare così, fino al valore a=8: in questo caso abbiamo l’unica possibilità 8999. Il numero delle soluzioni è allora dato dalla somma 8+7+6+…+2+1 = 36.
Solo cinque operazioni
C’è un’unica soluzione: [(14-4)×3:2+1]×125 = 2000.
Somma in orizzontale e in verticale
Le caselle della griglia sono 16. Se ad ogni casella, occupata o no da un gettone, associamo il numero dei gettoni che si incontrano sulla sua orizzontale e sulla sua verticale, otteniamo almeno 64 = 16×4. Supponiamo ora che tutte le caselle siano occupate da un gettone e contiamo per ogni casella i gettoni che si incontrano in orizzontale e in verticale: ciascun gettone viene contato 7 volte. Il più piccolo multiplo di 7 maggiore di 64 è 70, che corrisponde a 10 caselle occupate e 6 vuote.
Quanti sono?
I numeri in questione sono della forma abbc con 0 < a < b e b > c. Per il nostro ragionamento, facciamo “perno” sulla cifra b. Per b=9, a può prendere 8 valori e c 9 (0 incluso): in tutto abbiamo 72 possibili soluzioni. Per b=8, abbiamo 7×8=56 soluzioni. E così via. In totale, abbiamo che il valore richiesto è 8×9+7×8+6×7+…+2×3+1×2 = 240.
Quadrati e rettangoli a confronto
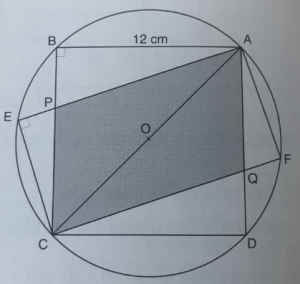
Il lato del quadrato misura 12 cm. L’area del rettangolo (con riferimento alla figura) può calcolarsi come a(ABCD)-2a(ABP)+2a(PEC) = 96+2a(PEC). Rimane allora da calcolare l’area del triangolo PEC.
La somma delle aree dei due triangoli (uguali) ABP e CDQ vale 144-96 = 48 cm2.
Quindi ciascuna area vale 24 cm2 e risulta BP=DQ= 4 cm, CP=AQ=8 cm. Dal teorema di Pitagora, applicato al triangolo ABP, si ottiene AP=4√10 cm. Infine, i triangoli ABP e EPC sono simili con rapporto di proporzionalità dato da √(2/5). Si deduce che l’area del triangolo PEC è data da 24×2/5 = 9,6 cm2. L’area del rettangolo AECF vale pertanto 96+2×9,6 = 115,2 cm2.
Classifiche di Tappa:
CE-CM
| Posizione | Cognome e nome | Punti |
| 1 | BRUSETTI LEILA | 50 |
| 2 | CATENA NICOLA | 45 |
| 3 | FORLIZZI FIAMMA | 42 |
C1
| Posizione | Cognome e nome | Punti |
| 1 | BARBANOTTI MATHEO | 50 |
| 2 | SARDAR TASIN | 45 |
| 3 | FARINA ANDREA | 42 |
| 4 | DE IOVANNA PAOLO | 40 |
| 5 | CAMPAGNARI NICOLA | 39 |
| 6 | AMBROSIO RICCARDO | 38 |
L1
| Posizione | Cognome e nome | Punti |
| 1 | PANAIOTTI COSIMO | 50 |
| 2 | MARINO GAIA | 45 |
| 3 | ROSCIANO SILVIA | 42 |
| 4 | CAMPAGNARI ASIA | 40 |
L1plus-L2-GP
| Posizione | Cognome e nome | Punti |
| 1 | CHINI PAOLO | 50 |
| 1 | PANTI FABRIZIO | 50 |
| 3 | MAZZOLENI RUBEN | 42 |
| 4 | QUATTROCCHI SALVATORE | 40 |
| 5 | PEDROLI ROBERTO | 39 |
| 6 | MACCHIA GIOVANNI | 38 |
| 7 | RICCARDI CLAUDIO | 37 |
| 8 | BRIOSCHI MARCO | 36 |
| 9 | BERTOLUCCI GIACOMO | 35 |
| 9 | FOLCHI GIANNI | 35 |
| 11 | STEFANONI MONICA | 33 |
| 12 | CARRARA CARLO | 32 |
| 13 | PASQUETTO CATERINA | 31 |
| 14 | LANDI GIUSEPPE | 30 |
| 15 | FENZI LUCA | 29 |
| 16 | LAI RAFFEALLA | 28 |
| 17 | MATTEU ANTIOCO | 27 |
| 18 | MORANDI BENEDETTO | 26 |
| 19 | ALLOGGIO GIOVANNI | 25 |
| 20 | BOSA RICCARDO | 24 |
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
3 risposte
Quando sarà pubblicata la classifica generale? Grazie arrivederci a settembre, Angela Bevilacqua.
Salve, riguardo al problema della categoria C2 somma in orizzontale e verticale, come devono essere disposti i 10 gettoni sulla griglia?
Buongiorno, in orizzontale o verticale