Modelli matematici: l’importanza del simulare

Per determinare le leggi fisiche, Galileo, Newton e i loro epigoni effettuavano misure sperimentali (la velocità di un corpo, la sua massa ecc.) e formulavano relazioni matematiche fra questi dati. Se i risultati che davano queste relazioni erano in buona approssimazione coerenti con quelli osservati negli esperimenti, divenivano leggi fisiche. Queste relazioni offrivano un modello matematico del fenomeno naturale. Per molto tempo, i principali modelli usati sono ricorsi alle equazioni differenziali, che esprimono leggi descrittive di un fenomeno in termini di come cambiano certe quantità nel tempo. Per esempio, Newton ha espresso la legge di raffreddamento di un corpo nel modo seguente: “Il tasso di perdita di calore di un corpo è proporzionale alla differenza fra la temperatura dell’ambiente e quella del corpo”. Supponiamo, all’istante t, che la temperatura dell’ambiente sia A e di avere un corpo alla temperatura T(t). Questo simbolo si legge “T di t” e denota la dipendenza di T da t. Newton afferma che la differenza di temperatura nel corpo fra l’istante t e l’istante t+1 è data da ΔT = k(A–T(t)). Cioè è proporzionale, con una costante di proporzionalità k, alla differenza fra la temperatura dell’ambiente e quella del corpo all’istante t (la lettera greca Δ indica tipicamente una differenza). Questa formulazione della legge fisica consente, con i metodi del calcolo differenziale introdotti proprio da Newton e da Leibniz, di risolvere l’equazione differenziale corrispondente e determinare il valore di T(t) per ogni istante t in un certo intervallo di tempo. Dunque, il modello non solo consente di formulare una legge che descrive un fenomeno naturale ma fornisce anche gli strumenti per capirne l’andamento nel tempo e quindi prevederlo. Le equazioni differenziali non si applicano solo in fisica ma in tutte le scienze. Un esempio classico in ecologia è il modello di Lotka-Volterra, che descrive la dinamica di due specie come le volpi e i conigli che condividono un territorio. Le due popolazioni interagiscono in quanto le volpi mangiano i conigli facendone diminuire il numero. I conigli, invece, cercano di sfuggire alle volpi e, se ci riescono, le fanno morire di fame e quindi ne fanno calare il numero. Se indichiamo con C(t) e V(t) il numero di conigli e volpi rispettivamente all’istante t e con ΔC e ΔV i tassi di crescita di queste popolazioni, ΔC aumenta in proporzione alla popolazione C(t) corrente (secondo un tasso di incremento demografico) ma diminuisce in modo proporzionale al prodotto C(t)×V(t) perché i conigli diminuiscono se incontrano le volpi e gli incontri sono proporzionali al prodotto della numerosità di entrambe le popolazioni: meno si è e meno ci si incontra! In formule: ΔC = a×C(t) – b×C(t)×V(t) dove a e b sono costanti di proporzionalità. Al contrario, le volpi aumentano proporzionalmente alla quantità C(t)×V(t), le possibilità di incontro con i conigli, mentre diminuiscono proporzionalmente alla quantità V(t) perché più predatori ci sono e più concorrenza si fanno. La formula del tasso di incremento della popolazione di volpi è quindi ΔV = c×C(t)×V(t) – d×V(t), dove c e d sono costanti di proporzionalità. Questa coppia di equazioni definisce un sistema di equazioni differenziali le cui soluzioni si possono scrivere esplicitamente: mostriamo il tipico andamento dei valori di C(t) e V(t) nella Figura 1.

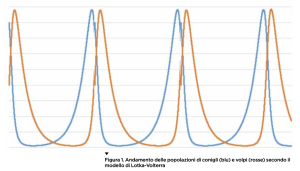
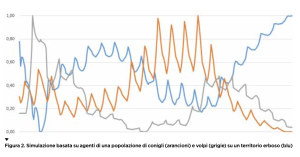
Partendo da una situazione in cui i conigli sono il doppio delle volpi, la popolazione di queste ultime aumenta per abbondanza di cibo e quella dei conigli diminuisce fino a scarseggiare. La conseguenza è che le volpi iniziano a morire di fame, il che alla lunga farà aumentare di nuovo i conigli e così via in una oscillazione continua delle due popolazioni. Una sorta di fuga matematica fra predatore e preda. Introducendo più specie in competizione e altri elementi del sistema reale, il modello si complica e non è più facile risolvere le equazioni, che esibiscono anche un comportamento caotico. Ma, da qualche decennio, esistono modelli alternativi per descrivere i fenomeni naturali: i modelli basati su agenti (agent-based model) che non modellizzano il sistema con una legge matematica ma provano a simularlo in forma semplificata all’interno di un computer. Per mettere in piedi una tale simulazione si programma un certo numero di “agenti” di vario tipo (che gli informatici chiamano oggetti) e si ripete per un certo numero di volte l’intervallo di tempo nel quale vogliamo studiare il sistema: un ciclo in cui a ogni iterazione ciascun agente segue delle regole specifiche e interagisce con gli altri. Per esempio, volendo simulare la dinamica fra conigli e volpi su un certo territorio, avremo almeno due tipi di agenti: i conigli e le volpi. Ciascun agente è un singolo individuo con i suoi propri dati (l’età, la sazietà, la sua posizione nel territorio ecc.) che variano nel tempo. Oltre ai dati, l’agente ha delle regole (codificate nel software) che a ogni ciclo della simulazione ne determinano il comportamento, per esempio mangiare o venire mangiato, morire di vecchiaia, generare della prole ecc. Mentre un’equazione differenziale rende conto di come variano i parametri statistici sulle popolazioni (come il numero di individui), in un modello ad agenti si fanno evolvere direttamente i singoli individui che, a ogni ciclo, interagiscono fra loro secondo regole date e qualche elemento di casualità. Per esempio, non ogni incontro fra coniglio e volpe dà luogo a una predazione, magari questo accade solo il 40% delle volte, quindi l’evoluzione del sistema non è deterministica ma prevede anche fattori casuali. Nella simulazione occorre introdurre un ambiente nel quale far muovere i nostri agenti, che sarà un territorio di una certa estensione, e il fattore cibo per gli erbivori, per esempio introducendo un nuovo agente “erba”; quest’ultima occupa lo spazio fisico dove si muovono prede e predatori. Le regole che determinano a ogni ciclo della simulazione cosa fa un agente dipendono dal tipo di agente: per esempio, un animale ha una età e a un certo punto muore di vecchiaia. Nel frattempo, può dar luogo a prole e nutrirsi: i conigli di erba e le volpi dei conigli. L’erba cresce, si espande nel territorio e muore quando un coniglio la mangia. Il territorio per semplicità potrebbe essere rappresentato da un tabellone, un po’ come quelli della battaglia navale, in cui in ciascuna casella può esistere dell’erba, un coniglio, una volpe o nulla. Questa descrizione un po’ sommaria può essere programmata in un computer in modo più o meno facile (usando “linguaggi orientati agli oggetti” è più semplice, si tratta di linguaggi inventati proprio per fare simulazioni). Poiché in una simulazione si introducono sempre dei fattori casuali, per esempio dove l’erba si propaga nel territorio, dove si spostano gli animali ecc., è possibile lanciare moltissime simulazioni sugli stessi dati iniziali e vedere che cosa succede in media oppure variare i dati iniziali e appurare la sensibilità del sistema a queste variazioni. Solitamente, nei sistemi complessi variazioni anche piccole determinano dinamiche completamente diverse (il celebre fenomeno della non linearità). Usando una simulazione con agenti si può verificare se le ipotesi semplificative del modello (codificate nel comportamento degli agenti e nei vincoli ambientali) offrono un riscontro empirico, confrontandolo per esempio con i dati sulle popolazioni di conigli, volpi ed erba in un certo territorio misurate sperimentalmente. Se il modello è coerente con queste evidenze, possiamo anche supporre che le conclusioni che se ne traggono ci dicano qualcosa sul sistema reale che stiamo modellizzando. Per esempio, nella Figura 2 vediamo il risultato di una simulazione in cui, su un territorio quadrato interamente erboso di 10.000 caselle, ci sono inizialmente 600 conigli e 300 volpi. Nella simulazione abbiamo considerato vite medie diverse per conigli e volpi e anche diversi periodi riproduttivi, tutte caratteristiche non codificate nel modello di Lotka-Volterra. Le curve tracciate nella figura sono state “normalizzate” fra 0 e 1 per essere confrontabili. Vediamo che ci sono sempre oscillazioni ma di due tipi, alcune di “lungo periodo”, altre di frequenza maggiore. In ogni caso, la popolazione dei conigli in arancione e quella delle volpi in grigio si alternano inseguendosi nella fuga che avevamo visto nella sua matematica regolarità nel modello di Lotka-Volterra. Le oscillazioni più frastagliate della simulazione somigliano molto di più ai dati reali. Inoltre, la quantità d’erba, la curva blu, risulta “anticorrelata” alla popolazione dei conigli, cioè maggiore quest’ultima e minore la prima, e viceversa. Sono risultati abbastanza scontati ma il fatto che siano emersi da una simulazione al computer rende conto della potenza di questi metodi. Non sappiamo se sarebbero piaciuti a Galileo e Newton, ma offrono una nuova e notevole arma a economisti, sociologi, antropologi nel loro quotidiano confronto con la complessità del reale.