L’intelligenza artificiale va alle gare (di matematica)

Prima dell’avvento dei computer e delle calcolatrici, ci si affidava ai calcolatori umani per conti che sembravano lunghi e soprattutto generatori di errori durante il loro svolgimento. In effetti, il termine “computer” esisteva da prima dell’invenzione, negli anni Quaranta, dei primi elaboratori elettronici digitali e designava proprio una categoria professionale specializzata nel fare calcoli a mano, l’unico modo possibile all’epoca! La professione era in auge già alla metà del Settecento, quando i calcoli astronomici erano ormai abbastanza complicati da richiedere tempo e sforzi che gli astronomi non potevano permettersi. Era una professione spesso praticata da donne, perché si trattava dell’unica possibilità che avevano all’epoca di lavorare in un settore scientifico. Oggi, nessuno potrebbe competere con un computer in una gara di calcoli, per l’ottimo motivo che i computer sono costruiti e programmati appositamente per farli meglio di qualsiasi essere umano. Ma nessuno di noi si farebbe venire un complesso di inferiorità per questo o troverebbe inquietante la cosa. Invece, quando si tratta di attività cognitive che ci paiono più complesse e misteriose, gli atteggiamenti cambiano. Prendiamo per esempio i LLM (Large Language Model) saliti alla ribalta delle cronache con l’avvento di ChatGPT. Si tratta di programmi, estremamente complessi, che riescono a generare testi in una lingua umana in risposta a testi prodotti da noi umani (o anche da altri LLM). Possiamo fare una domanda a ChatGPT, lui ci risponde e, nel farlo, utilizza la conoscenza di tutto il materiale testuale che si può scaricare da Internet. La potenza di fuoco di questi modelli è tale che non dovremmo stupirci se riescono a rispondere alle nostre richieste in modo spesso preciso e puntuale. E tuttavia, questo fatto crea molto stupore e anche inquietudine. Perché, se un computer riesce a moltiplicare numeri a 20 cifre in una frazione di secondo, la cosa non ci sconvolge mentre se riesce a comporre un testo in una nostra lingua sì? Probabilmente, perché non riteniamo il calcolo o l’esecuzione di un algoritmo un compito cognitivamente significativo. Se un computer riesce a fare calcoli molto veloci e precisi, diciamo che, in fondo, fa una cosa meccanica, nella sua natura. Se, invece, risponde in modo circostanziato a una domanda, esprime un parere, offre un suggerimento, ci pare che faccia qualcosa nella natura umana, non nella natura meccanica. I filosofi si sono posti da tempo queste domande e alcuni di loro hanno azzardato delle risposte, come John Searle con il suo esperimento mentale della “stanza cinese” [vedi box sotto]. Queste spiegazioni, convincenti o meno, tentano di ridurre quel che fa un computer a quel che sa fare, cioè calcoli ed elaborazioni algoritmiche. Per non parlare del fatto che il linguaggio potrebbe essere un fenomeno spiegabile algoritmicamente anche per come lo trattiamo noi. Ma la comprensione e il ragionamento si trovano su un livello superiore. All’epoca in cui Searle ha formulato l’esperimento mentale della stanza cinese, il suo obiettivo era mostrare che il linguaggio è un indicatore limitato dell’intelligenza umana e che l’uomo nella stanza cinese può produrre un testo in una lingua che non conosce solo seguendo delle istruzioni anche molto complesse e lunghe. Tuttavia, ragionamento e deduzione sono una cosa diversa: è vero che le esprimiamo nel linguaggio ma siamo convinti che possano prescindere da esso. La logica simbolica, per esempio, riesce proprio a esprimere deduzioni e ragionamenti in un linguaggio artificiale e non nel linguaggio naturale. L’esempio principe di deduzione è ovviamente la deduzione matematica. Il più antico, celebre e per molti versi stupefacente esempio di deduzione e ragionamento sono gli Elementi di Euclide, il più grandioso monumento a noi pervenuto della matematica ellenistica. La prosa degli austeri libri che compongono gli Elementi è sintetica ed essenziale (all’epoca non si usavano ancora i simboli matematici) e le dimostrazioni sono accompagnate da disegni che chi legge può tenere presenti per meglio comprendere i ragionamenti deduttivi. Sembra essere quanto di più lontano da ciò che un computer possa fare. Eppure, di recente, DeepMind – la divisione di ricerca e sviluppo di Google sulle tematiche dell’Intelligenza artificiale – ha realizzato AlphaGeometry, un software che è in grado di risolvere problemi di geometria paragonabili a quelli degli Elementi di Euclide e anche più sofisticati. Come già era accaduto con AlphaGo, l’IA che nel 2015 ha battuto i più grandi campioni del mondo di questo difficilissimo gioco da tavolo, il Go appunto, Google ha creato un software di Intelligenza artificiale per un compito specifico. Qualche anno dopo, da AlphaGo è stato creato AlphaGoZero che, anziché utilizzare partite reali di Go per imparare a giocare, utilizza partite generate da “lui” stesso e poi AlphaZero che, con le stesse tecniche, gioca a scacchi in modo ovviamente impareggiabile. Nel caso di AlphaGeometry non si tratta però di risolvere rompicapi che, per quanto abbiano una combinatoria immensa di casi possibili, sono pur sempre dei giochi con regole relativamente semplici. Qui si tratta di risolvere problemi di geometria, un compito che richiede capacità riflessiva e deduttiva e nel quale molti di noi erano tutt’altro che abili alle scuole dell’obbligo! Come è stato possibile? A dire il vero, il sogno di creare programmi per computer che dimostrassero teoremi geometrici è stato coltivato da molto tempo. I primi tentativi risalgono agli anni Cinquanta del secolo scorso, quando l’informatica era ancora nella propria infanzia. Negli anni Sessanta si fecero diversi progressi teorici che, all’atto pratico, non diedero frutto. All’epoca i computer avevano capacità di memoria e di calcolo milioni di volte inferiori a quelle odierne. Negli anni Settanta si proposero diversi dimostratori automatici di teoremi, come il sistema di Boyer-Moore, che alimentarono la ricerca fino agli anni Ottanta. Dopo questa epoca eroica, ci si orientò verso l’assistenza nelle dimostrazioni di teoremi realizzando programmi per computer che aiutassero i matematici a verificare se, per esempio, tutta la casistica fosse stata esaurita in una dimostrazione o se, invece, non ci fossero buchi o errori che si potessero individuare con strumenti automatici. I metodi di questi sistemi erano completamente diversi da quelli che sono alla base dei LLM: questi ultimi usano metodi statistici e numerici, laddove i dimostratori di teoremi usavano metodi algebrici e logici. In particolare, questi dimostratori usano un “motore deduttivo” che alimentano con gli assiomi e con altri teoremi nella speranza di fargli dedurre teoremi nuovi. AlphaGeometry fonde questi due approcci in un’architettura ibrida, che comprende una componente linguistica, data da un LLM che traduce il testo del problema in una forma adatta al sistema algebrico-logico, il quale tenta una soluzione e, se non la trova subito, si fa aiutare dal LLM.

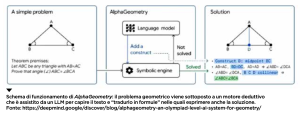
Questo software è stato in grado di risolvere problemi delle Olimpiadi matematiche del 2015 che molti di noi faticherebbero a risolvere senza consultare un libro o pensarci un bel po’. Un aspetto interessante, che è un marchio di fabbrica dei software Alpha di Google, è che gli esempi sui quali il sistema si addestra sono generati automaticamente. Come nel caso delle partite di Go, anche i problemi di geometria possono essere generati in quanto la teoria consente di dare dei criteri per stabilire se un problema è stato risolto o meno. Per capire questo punto, immaginiamo di generare figure a caso secondo certi criteri: ad esempio, un cerchio inscritto in un triangolo, poi di dare dei nomi a luoghi significativi di questa figura, per esempio dove il cerchio tocca i lati del triangolo e i vertici del triangolo, e infine di generare, usando regole geometriche predefinite, tutte le proprietà che ci vengono in mente per questa figura. Poi ne scegliamo una e chiediamo di dimostrarla. Quello che AlphaGeometry fa è esercitarsi a risalire dalla proprietà alla catena di relazioni che l’hanno generata partendo dalla figura che è nota a chi ha generato la proprietà e che quindi può verificare l’esattezza della risposta. In questo processo apprende come invertire i ragionamenti geometrici per poi utilizzare quel che ha appreso su casi mai visti prima. I risultati sono sorprendenti, ma alla fine nemmeno troppo, tenendo conto che un LLM senza l’ausilio del motore deduttivo riesce già soltanto sulla base dei numerosissimi testi matematici che ha letto a imbastire una risposta per semplici problemi. Potete provare con la versione gratuita di ChatGPT, o semplicemente ispezionare questo dialogo che trascrivo dal mio cellulare:

LA STANZA CINESE DI SEARLE

Supponiamo di chiudere un uomo in una stanza che abbia due finestre: dalla finestra di sinistra qualcuno può inserire un testo in cinese che l’uomo prende; dalla finestra di destra l’uomo può passare all’esterno un testo scritto da lui. Supponiamo che l’uomo possa fotocopiare e ritagliare i testi che riceve, per esempio ritagliarne una parte, e abbia della colla e quanti fogli vuole per incollare i ritagli sul foglio che poi passerà all’esterno. L’uomo ha anche a disposizione un elenco lunghissimo di regole, per esempio scritte su un computer o in volumi a sua disposizione, e molto, moltissimo tempo. Quando un foglio gli viene sottoposto, l’uomo ne esamina i caratteri: non sa nulla di ideogrammi cinesi ma segue le regole che gli sono date, ritaglia, incolla e produce un testo su un foglio che poi invia all’esterno. L’insieme di regole che l’uomo segue è un algoritmo, complicato a piacere; se vogliamo, lo stesso tipo di regole che un programma per computer può seguire.
Un osservatore esterno – scrive Searle – vedrebbe qualcuno inserire delle domande in cinese e vedrebbe anche uscire dalla stanza le risposte. Quindi penserebbe che all’interno della stanza vi sia qualcuno che sa il cinese e prepara le risposte. Ma non è così: l’uomo non sa il cinese, si limita a seguire delle istruzioni molto dettagliate e a fare copia/incolla.
Possiamo quindi dire che un programma per computer capisce, conosce o sa qualcosa o semplicemente dire che si limita a seguire istruzioni su un mucchio di dati?