È matematico il segreto per una guida sicura

Quando si parla di una curva di una strada, la prima figura geometrica a cui si pensa è la circonferenza. Così, siamo portati a immaginare una strada come una successione di segmenti rettilinei uniti da archi di cerchio. Questi “pezzi” di circonferenza, che possono avere dimensioni più o meno importanti, sono pensati in modo tale da consentire gli spostamenti da un punto di partenza a uno d’arrivo. Ebbene, quanto abbiamo appena detto non è quello che si verifica nella realtà della progettazione stradale che deve avere a cuore soprattutto la sicurezza di chi viaggia. In questo contesto, il progettista stradale viene assistito dalla geometria differenziale e da un po’ di altra matematica.

IL PROBLEMA

Immedesimiamoci in una situazione tipica: dobbiamo percorrere un tratto di strada composto in parte da un rettilineo e in parte da una curva, un arco di circonferenza appunto. Ebbene, durante la percorrenza del tracciato ci troveremmo di fronte a una discontinuità geometrica causata dal fatto che percorriamo due elementi geometrici che hanno, nel loro punto di unione, una proprietà ben differente: la curvatura. In particolare, passeremmo da una parte di tracciato a curvatura nulla, cioè il rettilineo, ad un’altra parte con curvatura non nulla, la circonferenza. Che cosa succede fisicamente? A cavallo della discontinuità, il guidatore non è più in grado di viaggiare parallelamente all’asse stradale perché necessita di un tempo, anche se ridotto, per indurre il veicolo a percorrere il nuovo tratto: deve, cioè, sterzare! Questo in primis, ma poi, come seconda diretta conseguenza della presenza di questa discontinuità, si troverebbe a essere di colpo sollecitato da una forza centrifuga tanto più grande quanto più piccolo è il raggio della circonferenza che deve percorrere. Questa forza può compromettere significativamente la stabilità del veicolo in moto e causarne possibili sbandamenti, dettati anche dal fatto che, come guidatori, si è tentati di sterzare più del dovuto per assecondare la curva. È proprio qui che viene in aiuto la matematica attraverso il concetto di curvatura di una linea sul piano. Dato un suo punto qualsiasi, esiste una sola circonferenza che approssima la linea intorno a tale punto nel modo migliore possibile. Il suo raggio r è detto raggio di curvatura e il suo reciproco 1/r è quello che si chiama curvatura della linea nell’unico punto di contatto che ha con la circonferenza: 1/r è una misura della tendenza che ha una curva a discostarsi da un andamento rettilineo. Se il raggio della circonferenza è piccolo, la curvatura è grande e abbiamo a che fare con una linea molto “curva”. Se, invece, la circonferenza è grande, allora la curvatura è piccola e la linea si discosta poco dall’essere rettilinea. Il raggio di curvatura di una circonferenza coincide proprio con il suo raggio, mentre per una retta, per misurare la sua tendenza a “curvarsi”, dovremmo considerare un cerchio grandissimo, qualunque sia il punto che scegliamo in partenza, tanto grande da avere un raggio pari a infinito. Il raggio di curvatura di una retta o di un segmento è infinito. Fisicamente, vuol dire che una retta non ha tendenza a curvarsi. Tra tutte le possibili curve che potremmo pensare di disegnare, la clotoide si presta benissimo a risolvere il problema che abbiamo di fronte.

LA MATEMATICA DELLA CLOTOIDE

Detta anche spirale di Eulero o spirale di Cornu, dal nome di un fisico francese che nella seconda metà dell’Ottocento la utilizzò per alcuni suoi studi sulla diffrazione, la clotoide è una curva geometrica del piano. Può essere visivamente rappresentata su un piano cartesiano da una sorta di filo che, arrotolato attorno a due punti, va a formare due spirali. La sua caratteristica è di avere una curvatura linearmente variabile lungo la sua lunghezza. La clotoide può allora essere definita come il luogo dei punti per i quali il prodotto del raggio di curvatura r per la lunghezza t del tratto percorso da un punto origine è costante. Pertanto, per mantenere costante il prodotto, quando varia la lunghezza del tratto di interesse, varia anche il valore del raggio di curvatura punto per punto lungo la curva. Se chiamiamo A² la costante che la caratterizza, la clotoide è rappresentata dall’equazione A² = r × t.

LE APPLICAZIONI PRATICHE

La clotoide riesce ad essere un ottimo elemento di raccordo tra zone del tracciato a curvatura differente.
Per esempio:
– quando il guidatore sta entrando in curva, la clotoide raccorda la curvatura infinita del rettilineo a una curvatura finita dell’arco di circonferenza;
– analogamente, la cosa può accadere quando il guidatore esce dalla curva;
– in altri casi, la clotoide può fungere da raccordo tra due curve circolari percorse in verso opposto (clotoide di flesso) oppure nello stesso verso tra loro ravvicinate (clotoide di continuità).

In tutti questi casi, un arco di clotoide viene progettato principalmente per avere graduali variazioni della forza centrifuga che sollecita il veicolo, migliorare la percezione della strada, permettere una graduale variazione della marcia al guidatore,
che quindi ha tutto il tempo necessario per assecondare il tracciato durante la guida. Tuttavia, la maggior parte delle strade esistenti è realizzata mediante elementi in rettifilo e curva circolare che non hanno un elemento di raccordo, in quanto questa tecnica di progettazione non è applicata da sempre nella progettazione stradale. Dal punto di vista matematico, rispetto al filo intrecciato che abbiamo visto prima, solo una parte effettiva di clotoide viene di fatto utilizzata in campo di progettazione stradale. Questo perché fisicamente i raggi di curvatura hanno ordini di grandezza che difficilmente vanno al di sotto dei 100 metri. La scelta del raggio di curvatura degli archi di cerchio dipende da prescrizioni normative e dalle velocità di progetto dell’infrastruttura. Per visualizzare meglio il grafico della figura 1, facciamo uno zoom su una zona particolare (figura 2).

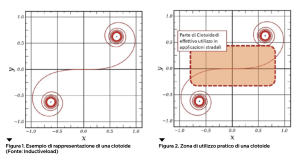
In questo modo si può intuire che le zone prossime all’origine del sistema di riferimento hanno una curvatura molto piccola.
Infatti, il punto nell’origine ha raggio di curvatura pressoché infinito. Mano a mano che si percorre la clotoide, diminuisce il raggio di curvatura e si possono quindi raccordare archi di cerchio di raggio sempre più piccolo. Ne viene da sé che più piccolo è il raggio da raccordare e più grande sarà il pezzo di clotoide da utilizzare per lo scopo. In alto nella figura 3, invece, è riportata una rappresentazione grafica di insieme di un’ipotesi di progetto stradale per collegare i punti posti tra le due stelle.

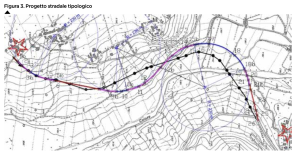
Il percorso viene descritto da un modello geometrico in cui si considerano 3 circonferenze con raggio di 230 metri, ma solo una parte di queste circonferenze è poi effettivamente utilizzata nel tracciato vero e proprio. Come si vede in figura 4, un arco di cerchio viene utilizzato per una fetta che è meno di ¼ di tutta la circonferenza. Una clotoide si interpone poi per garantire il raccordo con il successivo rettilineo, passando appunto da un raggio di curvatura di 230 metri a infinito. Pensateci durante il prossimo viaggio in auto!