I block-notes: La gaussiana

CHE COS’È

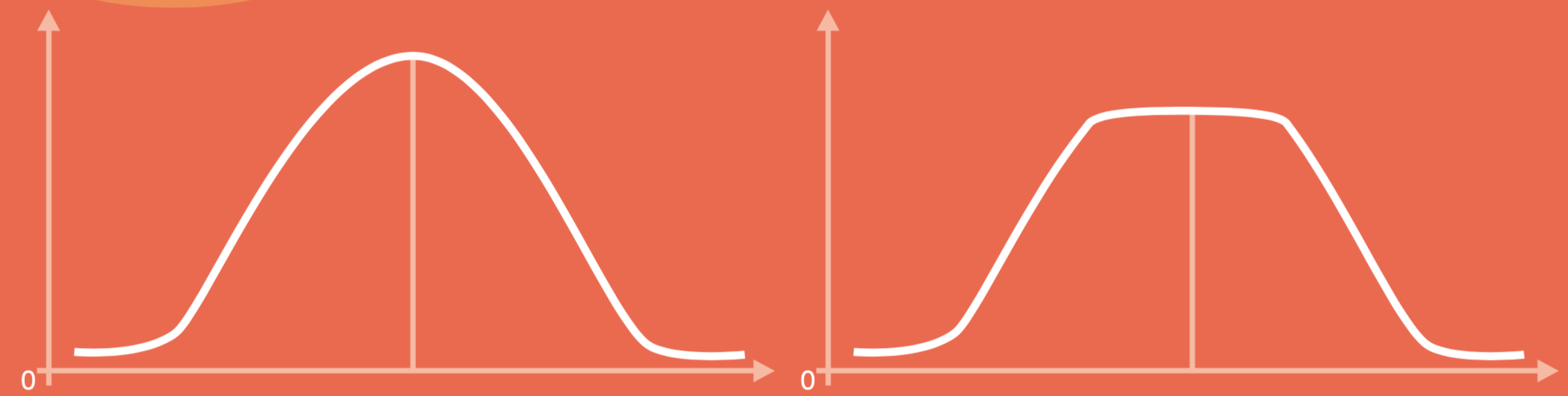
La gaussiana è una curva con la forma a campana, simmetrica rispetto al suo punto di massimo: inizia a salire lentamente, poi in modo sempre più deciso fino a raggiungere il valore massimo; da quel punto in poi scende in maniera simmetrica, prima rapidamente e in seguito quasi con dolcezza. C’è anche la versione con plateau (altopiano), quello di cui si è molto parlato a proposito del contagio. La curva a destra sale come nella descrizione precedente solo che, una volta raggiunto il valore massimo, non scende subito ma rimane per un tratto costante.

PERCHÉ SE NE PARLA TANTO IN QUESTE SETTIMANE DI CORONAVIRUS

La diffusione di un contagio porta a un numero di infettati che cresce all’inizio in modo esponenziale e poi in termini più contenuti. La sua velocità di propagazione segue invece un andamento gaussiano. Vediamo un esempio numerico: supponiamo che il contagio riguardi 1000 persone il primo giorno, 3000 in totale il secondo, 8000 in totale il terzo, 10000 in totale il quarto. Se rappresentassimo graficamente l’andamento del contagio con questi dati, avremmo un istogramma fatto da blocchi con altezze che almeno all’inizio crescono in modo esponenziale e poi continuano a crescere ma in modo meno deciso.

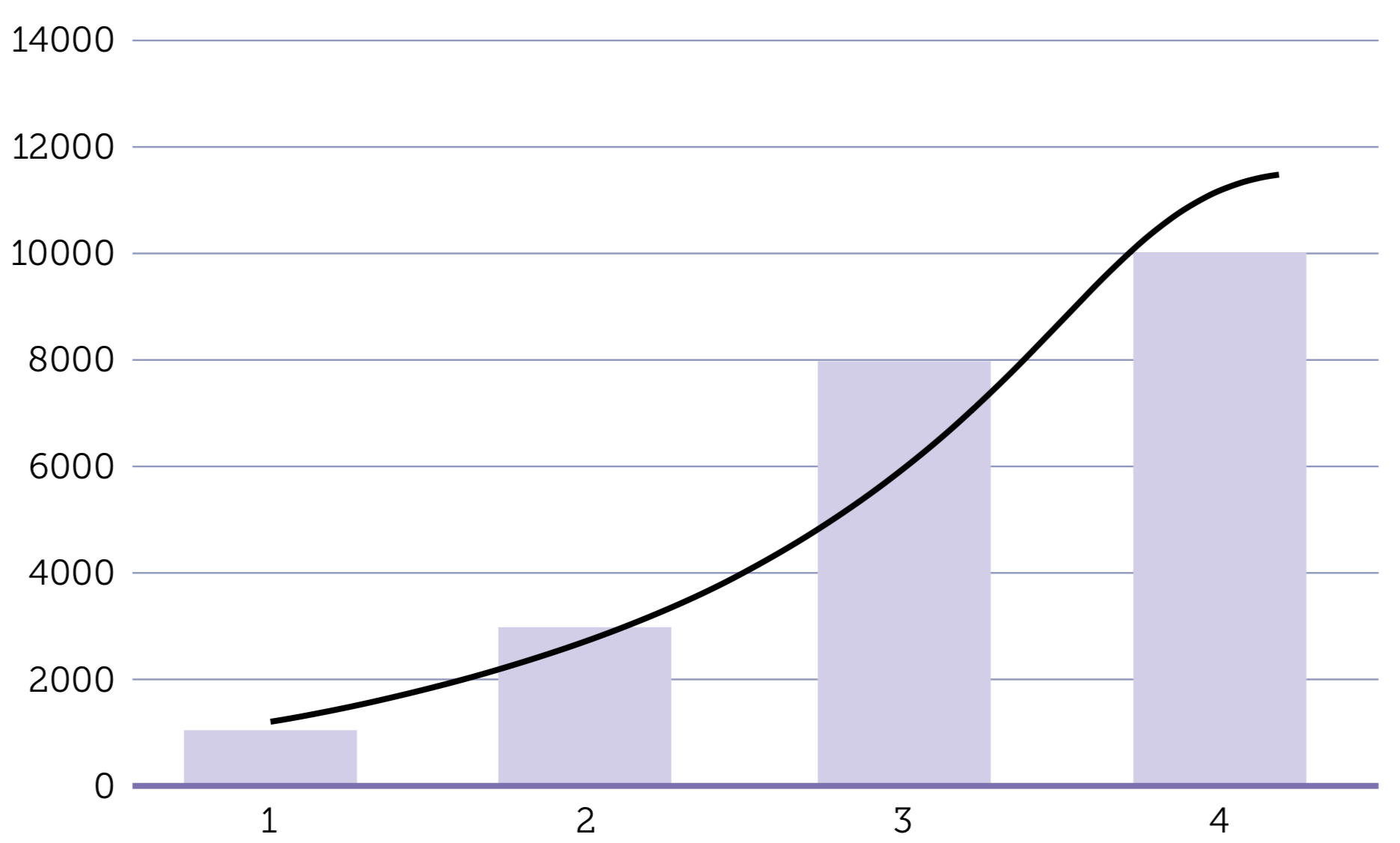
È la cosiddetta curva logistica con un andamento a sigmoide. Dà invece un’immagine più precisa, dell’andamento del contagio, il grafico basato sulla velocità di propagazione, ossia sulla differenza del numero totale di contagiati da un giorno all’altro. È proprio la velocità di propagazione del contagio che ha un andamento gaussiano.

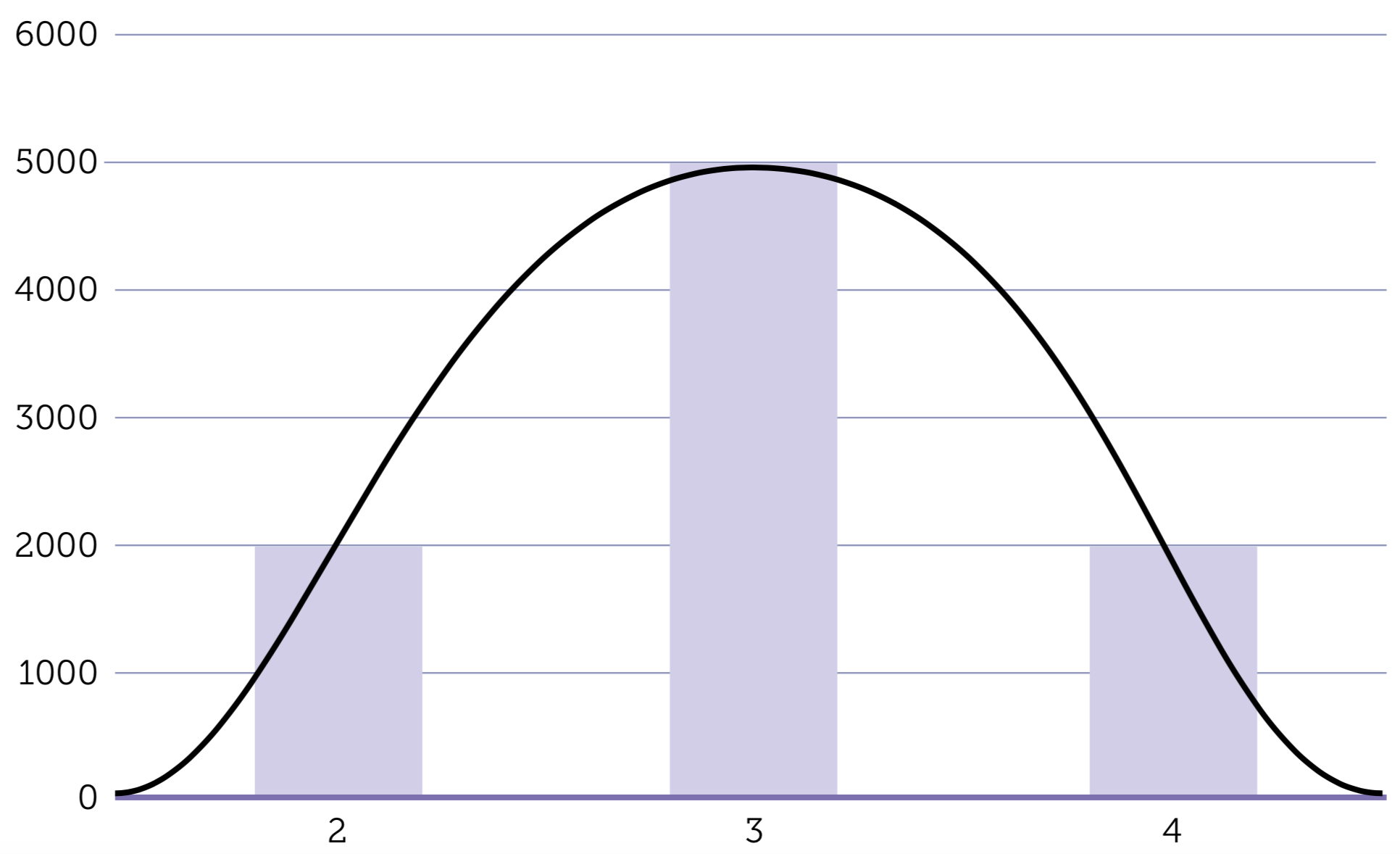
Il suo grafico permette di cogliere subito quando l’epidemia raggiunge il suo massimo e quando, magari dopo un tratto costante (il plateau), comincia a scendere.

Attenzione: non diminuisce il numero totale degli infettati. Quella che diminuisce è la velocità del contagio; i contagiati continuano ad aumentare ma con un tasso di crescita via via minore.

I matematici vedono nel disegno a campana il grafico della derivata f ’ della funzione f rappresentata nel grafico a sinistra: il tratto crescente della campana (f ’ crescente) corrisponde a una funzione f convessa (f ’’ positiva) che cresce in modo molto accentuato, esponenziale. Il punto di massimo di f ’ corrisponde a un punto di flesso della funzione f, quando questa da convessa diventa concava e la crescita continua ma con una velocità inferiore. L’eventuale plateau (f ’ costante), corrisponde a una crescita lineare.

PERCHÉ SI CHIAMA COSÌ

Il termine “curva gaussiana” viene dal matematico tedesco Karl Friedrich Gauss (1777-1855), che fu anche fisico e astronomo. Si occupò di algebra, aritmetica (dando una dimostrazione del teorema fondamentale dell’algebra per cui un polinomio di grado n ammette sempre n radici reali o complesse) e di geometria con gli studi sulla curvatura delle superfici, sulla rappresentazione geometrica dei numeri complessi e su quella che sarà la geometria non euclidea. Nel periodo degli studi astronomici formulò la legge della distribuzione degli errori casuali di misurazione esprimendola mediante la funzione e la curva che sarà poi chiamata appunto gaussiana.

LA MATEMATICA DEL PICCO E DEL PLATEAU

Ci sono diversi fenomeni che si sviluppano nel tempo (sistemi dinamici) con le stesse caratteristiche che abbiamo usato per descrivere il contagio del coronavirus. Bisogna capire quando raggiungeranno il picco e quale sarà questo valore di massimo. Potranno raggiungerlo con maggiore gradualità o con uno strappo deciso. Si procede allora sostanzialmente così:

a)  si ipotizza che il fenomeno si sviluppi in modo gaussiano;

b)  si impiegano i primi dati del fenomeno per scegliere i parametri numerici e una particolare forma di gaussiana che lo possa rappresentare;

c)  si utilizza questa particolare gaussiana per prevedere l’evoluzione del fenomeno (e capire, ad esempio, quando raggiungerà il suo picco);

d)  si usano i dati accumulati per precisare ulteriormente la forma della gaussiana e le sue caratteristiche numeriche.

È NORMALE IN PROBABILITÀ

La curva gaussiana è legata in probabilità alla “distribuzione normale” ed è rappresentata da una funzione esponenziale (del tipo e–x2) che dipende da due parametri: la media e la deviazione standard. Quando questi cambiano, la “campana” raggiunge il massimo in punti diversi. La gaussiana esprime in questo caso la concentrazione delle misurazioni effettuate attorno al loro valore medio. Questa distribuzione costituisce una buona approssimazione di altre distribuzioni di probabilità: il teorema del limite centrale afferma che la somma di un grande numero di variabili aleatorie indipendenti (cioè gli esiti di un particolare esperimento) si distribuisce proprio secondo una legge normale.